∫

∫是數學的一個積分，積分是微分的逆運算（拉丁文summa首字母的拉長，讀作：“sum”），即知道了函式的導函式，反求原函式。是用於求曲邊多邊形的面積，這巧妙的求解方法是積分特殊的性質決定的。

基本介紹

• 中文名：積分
• 外文名：∫
• 簡介：積分是微分的逆運算
• 在數學中：它被大量套用於求和

在數學中

在套用上，積分作用不僅如此，它被大量套用於求和，通俗的說是求曲邊多邊形的面積，這巧妙的求解方法是積分特殊的性質決定的。

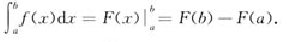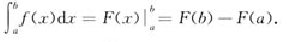牛頓萊布尼茲公式

一個函式的不定積分（亦稱原函式）指另一族函式，這一族函式的導函式恰為前一函式。

其中：[F(x) + C]' = f(x)

一個實變函式在區間[a,b]上的定積分，是一個實數。它等於該函式的一個原函式在b的值減去在a的值。

因為∫*dx=∫dx=x,所以積分符號∫與微分符號d相乘時可以抵消。

基本積分表：

(1)∫0dx=C

(2)∫adx=ax+C

(3)∫dx/x=ln|x|+C

(4)∫x^mdx=(1/(m+1))x^(m+1)+C(m≠-1，x>0)

(5)∫a^xdx=(1/lna)a^x+C(a>0,a≠1),特別地∫e^xdx=e^x+C

(6)∫cosxdx=sinx+C

(7)∫sinxdx=-cosx+C

(8)∫sec²xdx=tanx+C

(9)∫csc²xdx=-cotx+C

(10)∫secxtanxdx=secx+C

(11)∫cscxcotxdx=-cscx+C

(12)∫dx/sqrt(1-x²)=arcsinx+C

(13)∫dx/(1+x²)=arctanx+C

(14)∫dx/sqrt(1+x²)=arshx+C=ln(x+sqrt(x²+1))+C

(15)∫dx/sqrt(x²-1)=(|x|/x)arch|x|+C=ln|x+sqrt(x²-1)|+C

(16)∫dx/(1-x²)=(1/2)ln|(1+x)/(1-x)|+C

在英語中

[∫]在英語中是一種音標，常用於字母組 sh 。