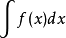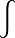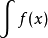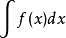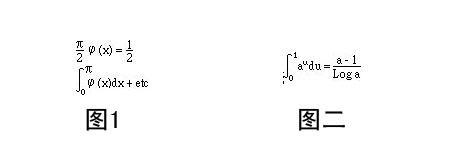積分符號（Signs for Definite Integrals）是萊布尼茨於1675年以“omn.l”表示l的總和（積分（Integrals）），而omn為omnia（意即所有、全部）之縮寫。其後他又改寫為 ∫，以“∫l”表示所有l的總和（Summa）。∫為字母s的拉長。此外，他又於1694年至1695年之間，於∫號後置一逗號，如 ∫,xxdx。至1698年，約．伯努利把逗號去掉，後更發展為現今之用法。
基本介紹
- 中文名：積分符號
- 外文名：Signs for Definite Integrals
- 提出者：萊布尼茨
- 提出時間：1675年
- 套用學科：數學
- 有關貢獻人：約．伯努利
積分符號使用,微積分歷史,積分符號來歷,
積分符號使用
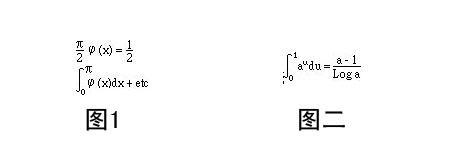
同時G．普蘭納採用了符號（圖二），而這符號很快便為數學界所接受，沿用至今。
微積分歷史
微積分學是微分學和積分學的總稱。從微積分成為一門學科來說，是在17世紀，但是，微分和積分的思想在古代就已經產生了。公元前3世紀，古希臘的阿基米德在研究解決拋物弓形的面積、球和球冠面積、螺線下面積和旋轉雙曲體的體積的問題中，就隱含著近代積分學的思想。
到了17世紀，有許多科學問題需要解決，這些問題也就成了促使微積分產生的因素。歸結起來，大約有四種主要類型的問題：第一類問題，是研究運動的時候直接出現的，也就是求即時速度的問題；第二類問題，是求曲線的切線的問題；第三類問題，是求函式的最大值和最小值問題。第四類問題是求曲線長、曲線圍成的面積、曲面圍成的體積、物體的重心、一個體積相當大的物體作用於另一物體上的引力。 17世紀的許多著名的數學家、天文學家、物理學家都為解決上述幾類問題作了大量的研究工作，如法國的費爾瑪、笛卡爾、羅伯瓦、笛沙格；英國的巴羅、瓦里士；德國的克卜勒；義大利的卡瓦列利等人都提出許多很有建樹的理論。為微積分的創立做出了貢獻。
17世紀下半葉，在前人工作的基礎上，英國大科學家牛頓和德國數學家萊布尼茨分別在自己的國度里獨自研究和完成了微積分的創立工作，雖然這只是初步的工作。他們的最大功績是把兩個貌似毫不相關的問題聯繫在一起，一個是切線問題（微分學的中心問題），一個是求積問題（積分學的中心問題）。
牛頓在1671年寫了《流數法和無窮級數》，這本書直到1736年才出版，它在這本書里指出，變數是由點、線、面的連續運動產生的，否定了以前自己認為的變數是無窮小元素的靜止集合。他把連續變數叫做流動量，把這些流動量的導數叫做流數。牛頓在流數術中所提出的中心問題是：已知連續運動的路徑，求給定時刻的速度（微分法）；已知運動的速度求給定時間內經過的路程（積分法）。
德國的萊布尼茨是一個博才多學的學者，1684年，他發表了現在世界上認為是最早的微積分文獻，這篇文章有一個很長而且很古怪的名字《一種求極大極小和切線的新方法，它也適用於分式和無理量，以及這種新方法的奇妙類型的計算》。就是這樣一片說理也頗含糊的文章，卻有劃時代的意義。他以含有現代的微分符號和基本微分法則。1686年，萊布尼茨發表了第一篇積分學的文獻。他是歷史上最偉大的符號學者之一，他所創設的微積分符號，遠遠優於牛頓的符號，這對微積分的發展有極大的影響。現在我們使用的微積分通用符號就是當時萊布尼茨精心選用的。
積分符號來歷
牛頓最早引進了微分和積分的符號，與牛頓同時研究微積分的萊布尼茨也引進了積分符號。相對牛頓的晚，但是優於牛頓的積分表達所以後人就採用萊布尼茨所發明的積分號了。
現行不定積分的定義為：若函式f(x)在某區間 I 上存在一個原函式F(x)，則稱F(x)+C（C為任意常數）為f(x)在該區間上的不定積分，記為
。
積分符號是微積分符號系統的重要組成部分。我們現在使用的微積分符號主要由德國數學家萊布尼茲（Leibniz）首先引進並使用的。在1675年10月29日的一份手稿中，他引入了我們現在熟知的積分符號“
”，這是求和一詞“sum”的第一個字母s的拉長。這是因為定積分表示的是一個無窮求和的過程，而歷史上首先出現的是定積分。稍後，在同年11月11日的手稿中，他又引進了微分記號dx。在1686年，萊布尼茲在發表的第一篇積分學論文中用
表示積分符號，後來則改為現在我們通用的
，在定義中我們可以看出
應該是一個整體的符號，代表求導的逆運算。然而，初學者很容易也較習慣地將整體符號拆開，將dx直接理解為微分。
