如果可以證明所有的無窮遠點共線,那么該線稱為無窮遠線。在仿射平面上,引入了理想元素 一 一 直線上的無窮點,一組平行線有共同的無窮遠點,不同的平行線組有不同的無窮遠點,平面上各方向的無窮遠點構成該平面上的無窮遠線。
基本介紹
- 中文名:無窮遠線
- 外文名:line at infinity
- 正文:可以證明所有的無窮遠點共線
- 推導:麥比烏斯的同胞普呂克也提出了
- 套用:對於任意圓錐曲線
原理

套用


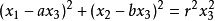



如果可以證明所有的無窮遠點共線,那么該線稱為無窮遠線。在仿射平面上,引入了理想元素 一 一 直線上的無窮點,一組平行線有共同的無窮遠點,不同的平行線組有不同的無窮遠點,平面上各方向的無窮遠點構成該平面上的無窮遠線。



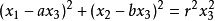


如果可以證明所有的無窮遠點共線,那么該線稱為無窮遠線。在仿射平面上,引入了理想元素 一一 直線上的無窮點,一組平行線有共同的無窮遠點,不同的平行線組有不...
無窮遠直線((line at infinity))亦稱假直線或理想直線。指歐氏平面上的一條假想直線,它是平面上所有直線上的無窮遠點的集合。為了區別起見,平面內原有的直線稱...
無窮遠平面,假平面或理想平面。歐氏空間中的一個假想平面,即空間中所有直線上的無窮遠點的集合。為區別起見,把空間中原有的平面稱為有窮平面、真平面或普通平面...
3種二次曲線與無窮遠直線的位置關係如圖1所示。圖1 由定義顯然可知,一條非退化二次曲線為拋物線的充要條件是它與無窮遠直線相切 [2] 。...
射影平面就是2維射影空間。它可以視為平面添上一條無窮遠直線。 它是代數幾何、射影幾何里最基本的對象。對射影平面的理解是從局部到整體的擴展過程。先從無窮...
在仿射平面上,每個三次曲線與無窮遠線有三個交點,必有一實交點(另外兩個也可以是實交點,也可以是共軛的虛交點)。交點處的切線即為漸近線,這樣我們必得到一個實...
例如,在射影平面上取一條直線作無窮遠直線,則在射影平面上保持無窮遠直線不變的自同構射影變換構成一個變換群,它是關於無窮遠直線的自同構群,同時它也是二位射...
在射影幾何里,兩條平行直線在無窮遠處相交,該點稱為無窮遠點。無窮遠點的...“如果兩個三角形對應頂點連線共點,那么對應邊的交點共線,反之也成立”,就是...
二維平面上的射影坐標系由不共線的四點定義,即O(原點),E(單位點),Ix(x軸上的無窮遠點)與Iy(y軸上的無窮遠點)定義,平面上任意一點A的射影坐標由兩個交...
如果再進一步,把無窮遠元素(點、線、面)和非無窮遠元素平等看待,不加區別,擴大空間就叫做射影空間。同樣,從擴大直線和擴大平面可以得到射影直線和射影平面。在射...
迷向直線(isotropic line)亦稱極小直線,是射影幾何的基本概念之一。指通過虛圓點的任意虛直線,迷向直線與無窮遠直線的交點一定是虛圓點。迷向直線構成以點(1,i...
因此,可定義(m, −n, 0)為對應nx+my= 0這條線之方向的無窮遠點之齊次坐標。因為歐氏平面上的每條線都會與透過原點的某一條線平行,且因為平行線會有相同...
的點,直線或平面加以區分,把無窮遠元素看成是特定的元素來對待,這樣的直線、平面和空間就是仿射的直線、平面或空間,這時把兩條交於無窮遠點的直線稱為平行線,...
射影空間是整體幾何最基本的研究對象之一。射影空間的概念最初產生於古典射影幾何。對於射影定理中的奇異情形(即有些直線相互平行的情形),為方便起見引入無窮遠...
對於射影定理中的奇異情形(即有些直線相互平行的情形),為方便起見引入無窮遠點的概念,即規定平面上每條直線上有一個無窮遠點,兩條直線平行就是相交於無窮遠點,...
又球與圓錐之交為圓,設以此圓所在平面π與π'之交為直線d(曲線為圓時d為無窮遠線),則d為準線。圖只畫了橢圓,證明對拋物線雙曲線都適用,即證,任一個切點為...
在射影空間中,成射影對應的兩個平面束對應平面的交線的軌跡是一個二階曲面。...對於射影定理中的奇異情形(即有些直線相互平行的情形),為方便起見引入無窮遠點...
復射影空間是實射影空間的推廣,即復歐氏空間添加無窮遠點構成的空間。添加了無窮遠點的複平面稱為一維復射影空間,記為CP1,推廣到n維,便得到n維復射影空間,它...
