定義
平方數也稱
正方形數,若
n為平方數,將
n個點排成矩形,可以排成一個正方形。
若將
平方數概念擴展到有理數,則兩個平方數的比仍然是平方數,例如,
。
若一個整數沒有除了 1 之外的
平方數為其因子,則稱其為無平方數
因數的數。
舉例
最小的50個完全
平方數為(OEIS中的數列A000290):
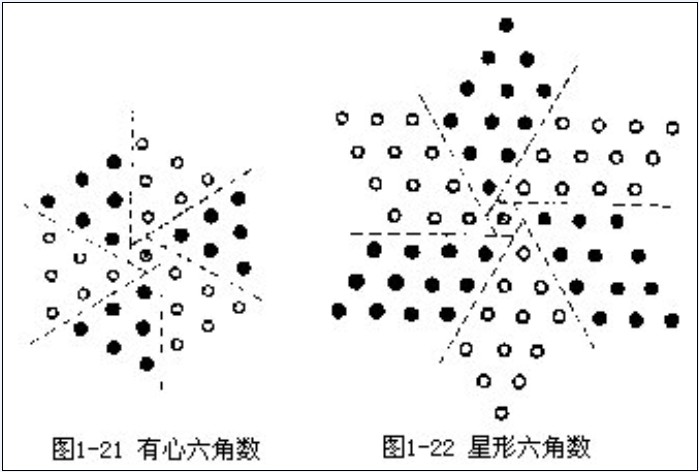 圖1:構成平方數的星形六角數
圖1:構成平方數的星形六角數12 = 1, 22 = 4 ,32 = 9, 42 = 16, 52 = 25, 62 = 36 ,72 = 49 ,82 = 64 ,92 = 81 ,102 = 100,
112 = 121, 122 = 144 ,132 = 169 ,142 = 196 ,152 = 225, 162 = 256, 172 = 289 ,182 = 324, 192 = 361 ,202 = 400,
212 = 441 ,222 = 484, 232 = 529 ,242 = 576, 252 = 625 ,262 = 676, 272 = 729 ,282 = 784 ,292 = 841, 302 = 900,
312 = 961, 322 = 1024, 332 = 1089 ,342 = 1156 ,352 = 1225, 362 = 1296 ,372 = 1369 ,382 = 1444, 392 = 1521 ,402 = 1600,
412 = 1681, 422 = 1764 ,432 = 1849, 442 = 1936, 452 = 2025 ,462 = 2116 ,472 = 2209 ,
482 = 2304 ,492 = 2401, 502 = 2500。
性質
一個
平方數是兩個相鄰三角形數之和。兩個相鄰
平方數之和為一個中心正方形數。所有的
奇數平方數同時也是中心八邊
形數。
四平方和定理說明所有
正整數均可表示為最多四個平方數的和。特別的,三個
平方數之和不能表示形如 4k(8m + 7) 的數。若一個
正整數可以表示因子中沒有形如 4k + 3 的素數的奇次方,則它可以表示成兩個
平方數之和。
奇數的平方除以4餘1,偶數的平方則能被4整除。
a2-b2=(a+b)(a-b)。
一個平方數是兩個相鄰
三角形數之和。兩個相鄰平方數之和為一個
中心正方形數。所有的奇數平方數同時也是中心八邊形數。
四平方和定理說明所有正整數均可表示為最多四個平方數的和。特別的,三個平方數之和不能表示形如 4(8
m+ 7) 的數。若一個正整數可以表示
因數中沒有形如 4
k+3 的素數的奇次方,則它可以表示成兩個平方數之和。
在
十進制中,平方數只能以 00,1,4,6,9 或 25 結尾:
若一個數以 0 結尾,它的平方數以 00 結尾,且其他數字也構成一個平方數;
若一個數以 1 或 9 結尾,它的平方數以 1 結尾,且其他數字構成的數能被 4 整除;
若一個數以 2 或 8 結尾,它的平方數以 4 結尾,且其他數字構成一個偶數;
若一個數以 3 或 7 結尾,它的平方數以 9 結尾,且其他數字構成的數能被 4 整除;
若一個數以 4 或 6 結尾,它的平方數以 6 結尾,且其他數字構成一個奇數;
若一個數以 5 結尾,它的平方數以 25 結尾,且前面的一位或兩位數字數字必定為 0,2,06,56 之一,25前面的數是
普洛尼克數。
表達式
方陣
著名數學家畢達哥拉斯發現有趣
奇數現象:將連續奇數相加,每次的得數正好就產生
完全平方數。 如:1 + 3(=2
2) + 5(=3
2) + 7(=4
2) + 9(=5
2) + 11(=6
2) + 13(=7
2)……在奇數和
平方數之間有著密切的重要聯繫。一個整數是完全平方數
若且唯若相同數目的點能夠在平面上排成一個正方形的點陣,使得每行每列的點都一樣多。
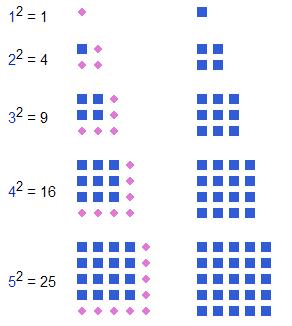 圖2:平方數
圖2:平方數通項公式
對於一個整數
n,它的
平方寫成
n2。n
2等於頭
n個正
奇數的和。在上圖中,從1開始,第
n個平方數表示為前一個平方數加上第
n個正奇數,如 5
2 = 25 = 16 + 9。即第五個平方數25等於第四個平方數16加上第五個正奇數:9。
遞推公式
每個完全
平方數可以從之前的兩個平方數計算得到,
遞推公式為 n
2 = 2(n − 1)
2 − (n − 2)
2 + 2。例如,2×5
2 − 4
2 + 2 = 2×25 − 16 + 2 = 50 − 16 + 2 = 36 = 6
2。
連續整數的和
完全
平方數還可以表示成
n2 = 1 + 1 + 2 + 2 + ... + n − 1 + n − 1 + n。例如,4
2 = 16 = 1 + 1 + 2 + 2 + 3 + 3 + 4。可以將其解釋為在邊長為 3 的矩形上添加寬度為 1 的一行和一列,即得到邊長為 4 的矩形。這對於計算較大的數的完全平方數非常有用。例如: 52
2 = 50
2 + 50 + 51 + 51 + 52 = 2500 + 204 = 2704。

 圖1:構成平方數的星形六角數
圖1:構成平方數的星形六角數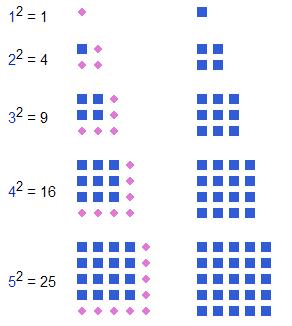 圖2:平方數
圖2:平方數
