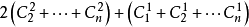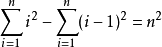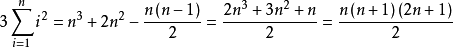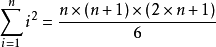平方和公式

平方和公式是一個比較常用公式，用於求連續自然數的平方和（Sum of squares），其和又可稱為四角錐數，或金字塔數（square pyramidal number）也就是正方形數的級數。

此公式是馮哈伯公式(Faulhaber's formula)的一個特例。

基本介紹

• 中文名：平方和公式
• 外文名：Sum of Squares
• 適用範圍：數學
• 類別：公式

公式

利用此公式可求得前n項平方和為：

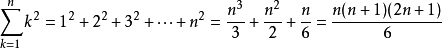
n	前n項平方和	n	前n項平方和	n	前n項平方和	n	前n項平方和	n	前n項平方和
1	1	6	91	11	506	16	1496	21	3311
2	5	7	140	12	650	17	1785	22	3795
3	14	8	204	13	819	18	2109	23	4324
4	30	9	285	14	1015	19	2470	24	4900
5	55	10	385	15	1240	20	2870	25	5525

n=26，27，28，29......時

前n項平方和和為：6201, 6930, 7714, 8555, 9455,
10416, 11440, 12529, 13685, 14910, 16206, 17575, 19019, 20540, 22140,
23821, 25585, 27434, 29370……

證明方法

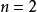
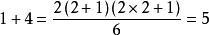
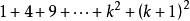
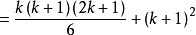
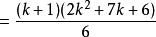
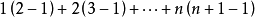
證法一　（歸納猜想法）：

1、 時，

2、 時，

3、設 時，公式成立，即

則當 時，

也滿足公式。

根據數學歸納法，對一切自然數n有 成立。

證法二 （利用恆等式 ）：

，

…………

.

求和得：

,

由於 （可由倒序求和得到）,

代入上式得：

整理後得：

證法三（ ） ：

令

=

=

因為

所以，

證法四　（排列組合法）：

由於 ，

因此我們有
=

由於 ， ，

於是我們有

證法五 （拆分，直接推導法）：

1=1

2²=1+3

3²=1+3+5

4²=1+3+5+7

...

(n-1)²=1+3+5+7+...+[2(n-1)-1]

n²=1+3+5+7+...+[2n-1]

求和得：

……(*)

因為前n項平方和與前n-1項平方和差為n²

代入(*)式，得：

此式即