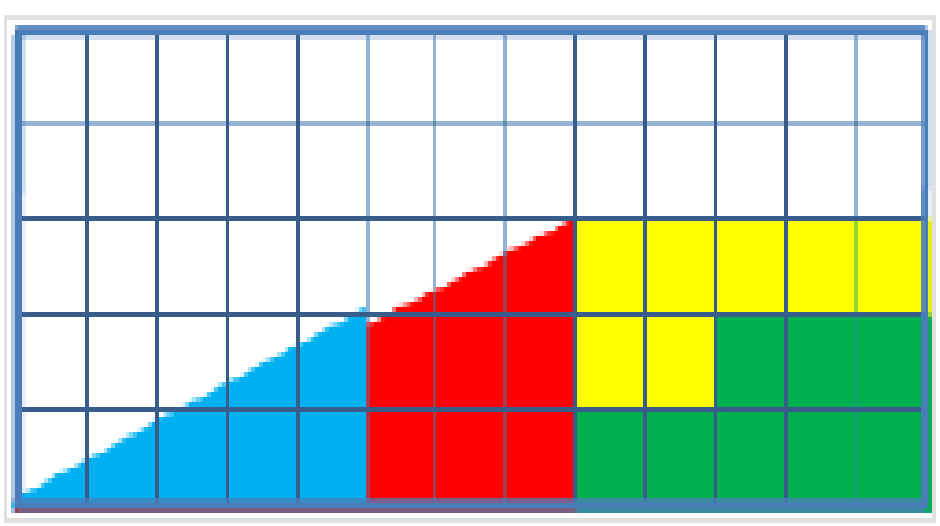
失蹤的正方形
相關詞條
- 失蹤的正方形
失蹤的正方形謎題是一種用於數學課的視覺錯覺,有助於學生對幾何圖形的思考。它描述了四個幾何圖形的兩種不同組合,都是13乘5的三角形,不過第二種拼法少了一個1...
- 馬丁·加德納
失蹤的正方形 德納總是能借其引出一些只有在大學才能學習到的數學理論,例如微積分、數列、拓撲學、群論、機率論等等。很多青少年正是因為加德納的趣味數學題才對數學...
- 智商導圖Ⅱ
075 失蹤的正方形076 圖形組合077 直線穿圈078 手巧的少婦079 字母與圓盤080 補充圖案081 觀察正方形3. 立體空間遊戲082 疊放次序...
- 中學生素質教育文庫
16.失蹤的正方形/43 17.籃球上的黑點/44 18.漆上顏色的立方體/44 19.最多可把餡餅切成幾塊?/44 20.數字無序化/45 21.這些圖形能一筆畫出來嗎?/...
- 心中無旁騖:提升注意力的思維遊戲
尋找正方形失去的數字尋找多米諾骨牌數三角形最後的彈孔相似性黑白棋子失蹤的正方形用“眼”估估看找數字十字架數圓點彌補缺憾五格六邊形...
- 國小數學課外讀物:數學真美妙
2.失蹤的正方形55 3.神機妙算“222”56 4.奇特的50之謎58 5.抹不掉的數字59 (五)數學趣題59 1.分牛59 2.哪邊球多?60 3.你能用圖形表示分...
- 聰明人玩的118個創新思維遊戲
遊戲4失蹤的正方形/11遊戲5用“眼”估估看/12遊戲6殘缺的棋盤/13遊戲7消失的顏色/15遊戲8最後一個/17遊戲9找數字/21遊戲10十字架/22...
- 逆挑戰:最高明數學思維的150個遊戲
遊戲11 失蹤的正方形 /17 第二章 簡單思維遊戲 /19 什麼是簡單思維 /19 遊戲12 製作旗幟 /21 遊戲13 套娃價格 /22 遊戲14 奇偶相同 /24 遊戲15...
- 走進理科王國:數學趣話
二、失蹤的正方形 三、幾何分割與藝術 四、幾何分割與複製磚 五、幾何分割定理 六、三等分角 七、幾何分割與完美矩形 八、尺規割圓 九、傅立葉分割...