映射與流形間某種規則相處狀態的刻畫.它推廣了映射在正則值處的性質,橫截性在動力系統理論中起著重要作用.
基本介紹
- 中文名:橫截性
- 外文名:transversality
- 所屬領域:數理科學
- 套用領域:動力系統理論等
定義
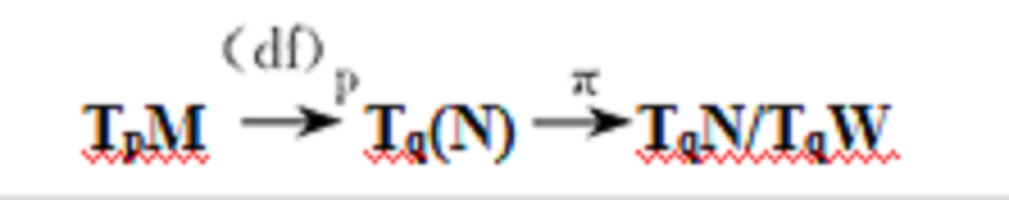




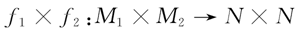











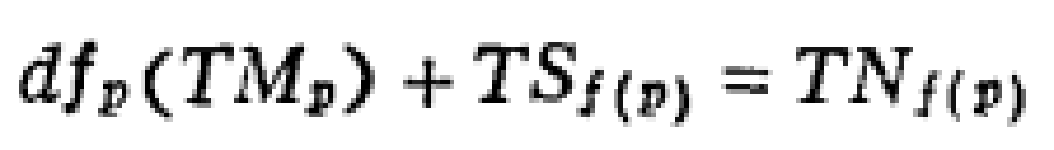
相關命題和推論

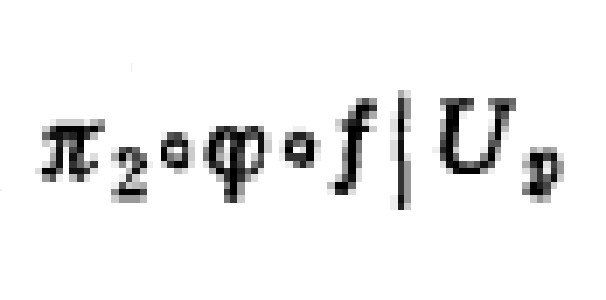



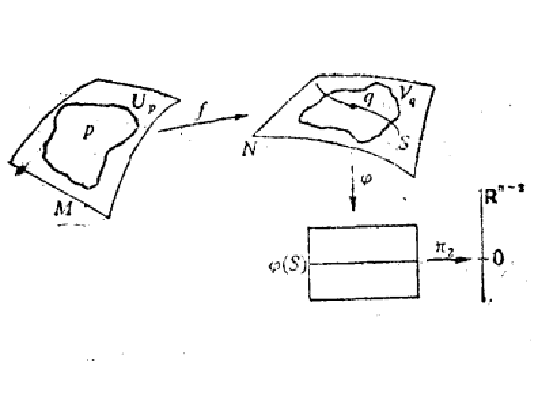
映射與流形間某種規則相處狀態的刻畫.它推廣了映射在正則值處的性質,橫截性在動力系統理論中起著重要作用.
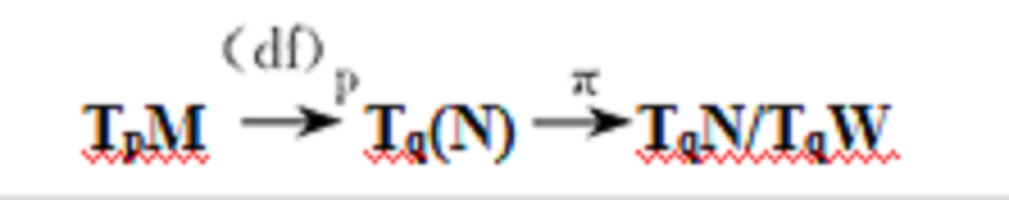




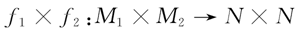











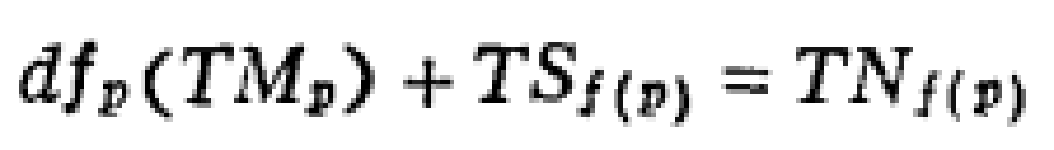

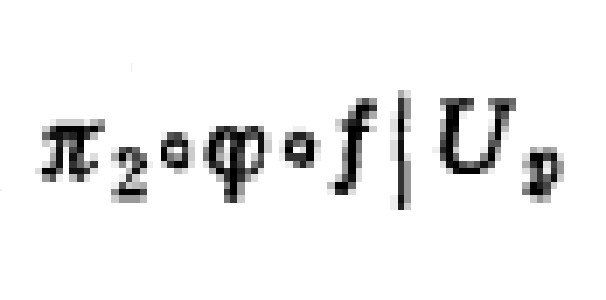



映射與流形間某種規則相處狀態的刻畫.它推廣了映射在正則值處的性質,橫截性在動力系統理論中起著重要作用...
托姆橫截性引理(Thorn transversality lemma)是關於橫截映射集的性質的一個引理。...... 托姆橫截性引理(Thorn transversality lemma)是關於橫截映射集的性質的一個...
托姆橫截性定理(Thom transversality theo-em)微分拓撲學的重要定理.它也是動力系統理論研究的重要工具.它表明流形之間具有橫截性的映射是“足夠普遍”的.設M,N都...
在數學中,橫截相交是描述空間如何相交的概念,並在一般的立場上發揮作用。 它形成了差分拓撲中通用交集法。 通過考慮交點處的交叉空間的線性化來定義。...
謝建華, 橫截性理論在碰撞振動系統結構穩定問題中的套用. 力學學報, 24(4), 480-487, 1992.謝建華, 振動錘的數學模型與全局分叉. 力學學報, 29(4), 456-...
1.3.4 兩種等價的定理形式1.4 正則值與橫截性1.4.1 Sard定理1.4.2 橫截性1.4.3 Thom橫截性定理1.5 向量叢與管形鄰域1.5.1 向量叢1.5.2 平凡叢的判別...
自由橫截性條件建立了平穩曲線的切線斜率與曲線λ的切線斜率的關係,這裡的自由端在曲線λ上移動,稱為變動端點,相應變分問題稱為變動邊界變分問題。...
2 橫截性3 橫截逼近定理4 關於映射的cr拓撲與cr意義下的逼近5 參數橫截性定理與涉及帶邊流形的定理附錄r sard定理的證明練習e...
上滿足線性橫截性條件若且唯若 (引進常微系統)定理4若 滿足線性橫截性條件,則它也滿足公理 。定理5若 在 中一個 下不變的閉子集A 上滿足線性橫截性條件,...
