基本介紹
定義

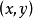


記法








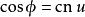
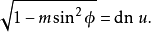

第一類不完全

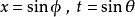


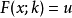
加法公式
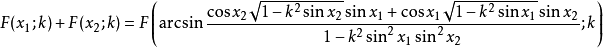
導數


第二類不完全


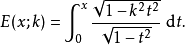
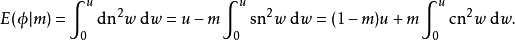

加法公式


性質


導數



第三類不完全



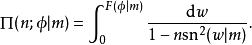
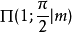
第一類完全

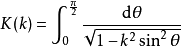



第二類完全
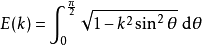
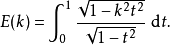

第三類完全
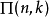
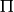
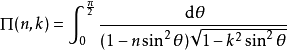

函式關係



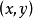










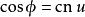
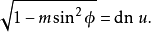


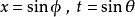


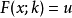
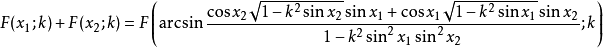




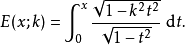
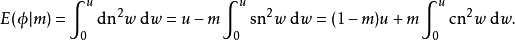











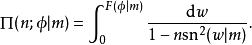
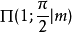

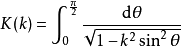



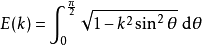
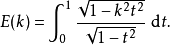

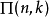
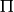
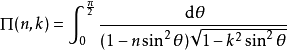


在積分學中,橢圓積分最初出現於橢圓的弧長有關的問題中。Guilio Fagnano和歐拉是最早的研究者。通常,橢圓積分不能用基本函式表達。這個一般規則的例外出現在P有重...
超橢圓積分其積分值完全由L本身的起始點和終點所確定,和Abel積分的一般情形一樣,任何超橢圓積分均可表示成一些初等函式和具有特殊形式的第一、二、 三類典範超橢圓...
勒讓德型橢圓積分(elliptic integral in Lege-ndre's form)亦稱不完全橢圓積分.橢圓積分的一種常用的標準形式...
外爾斯特拉斯型橢圓積分(elliptic integral inWeierstrass' form)是橢圓積分的另一種常用的標準形式。...
橢圓周長沒有精確的初等公式,但有非初等的橢圓積分形式的表達及其級數展開式。...... 橢圓周長沒有精確的初等公式,但有非初等的橢圓積分形式的表達及其級數展開式。...
雙周期的亞純函式。它最初是從求橢圓弧長時引導出來的,所以稱為橢圓函式。橢圓函式論可以說是複變函數論在19世紀發展中最光輝的成就之一。...
橢圓體(ellipsoid):橢圓圍繞它的長軸或短軸旋轉一周所圍成的幾何體...... 橢圓體(ellipsoid):橢圓圍繞它的長軸或短...其中E(φ,k)和F(φ,k)是橢圓積分...
阿貝爾積分,其中R(x,y)是x和y的有理函式,且存在二元多項式ƒ,使ƒ(x,y)=0。他還證明了關於上述積分之和的定理,現稱阿貝爾定理。...
第二類橢圓函式(elliptic function of the second kind)是橢圓函式(即第一類橢圓函式)的推廣之一,另外一種為第三類橢圓函式,是橢圓函式的進一步推廣。橢圓函式是雙...
第三類橢圓函式(elliptic function of the third kind )是橢圓函式(即第一類橢圓函式)的進一步推廣。橢圓函式是雙周期亞純函式的統稱。歷史上,橢圓函式是作為橢圓...
橢圓餘弦波(cnoidal wave)是一種淺水波動。在近海橢圓餘弦波波面形狀與斯托克斯波和擺線波相比更接近實際情況。該波動可用橢圓函式表達,也因此得名。當波高與水深的...
概述是一種幾何形狀。類似於橢圓。周長計算沒有公式,但有積分形式的表達: 最早由伯努利(那個不記得了)提出,歐拉發展 對這類問題的討論引出一門數學分支--橢圓積分...
在數學中,魏爾斯特拉斯橢圓函式又稱ρ函式,是格外簡單的一類橢圓函式,也是雅可比橢圓函式的特殊形式。卡爾·魏爾斯特拉斯首先研究了這些函式。...
橢圓面積公式:S=π(圓周率)×a×b,其中a、b分別是橢圓的半長軸,半短軸的長。橢圓面積公式屬於幾何數學領域。...
橢圓曲線是域上虧格為1的光滑射影曲線。對於特徵不等於2的域,它的仿射方程可以寫成:y^2=x^3+ax^2+bx+c。複數域上的橢圓曲線為虧格為1的黎曼面。Mordell...
雅可比橢圓函式是雙周期的亞純函式,屬於橢圓餘弦橢圓正切,與圓函式(三角函式)相似。...
雅可比橢圓函式的定義第一類橢圓積分 z=∫[(1-t^2)(1-k^2*t^2)]^(-1/2)dt (0~ω) 的反函式是雙周期的亞純函式,記作 ω=sn(z)=sn(z,k) 它...
橢圓函式論新基礎(Fundamenta nova theorizefunctionum ellipticarum)西方近現代數學著作.德國數學家雅可比(Jacobi,C. G. J.)著,1829年出版.雅可比與阿貝爾(Abel ,...
既然研究三角函式要比表示為不定積分的反三角函式容易得多,那么對應地研究橢圓積分的反函式(後來就稱為橢圓函式)不也應該比橢圓積分本身容易得多嗎?...
