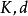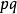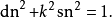基本介紹
雅可比橢圓函式的定義










| 函式 | 周期 | 零點 | 極點 | 留數 |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  | 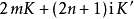 |  |
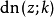 |  |  |  |  |
 與  是整數 | ||||
雅可比橢圓函式的性質
z | 0 | K/2 | K | iK'/2 | K+iK'/2 | iK' | K+iK' |
sn(z) | 0 | (1+k'^2)^(-1/2) | 1 | ik^(-1/2) | k^(-1/2) | ∞ | 1/k |
cn(z) | 1 | sqr(k'/(1+k')) | 0 | sqr((k+1)/k) | -sqr((k-1)/k) | ∞ | -ik'/k |
dn(z) | 1 | k'^(1/2) | k' | sqr(1+k) | sqr(1-k) | ∞ | 0 |
sn(mK+niK±z)誘導公式表
╲m n╲ | -1 | 0 | 1 | 2 | 2p |
-1 | -dn(z)/(k*cn(z)) | ±1/(k*sn(z)) | dn(z)/(k*cn(z)) | 負正1/(k*sn(z)) | |
0 | -cn(z)/dn(z) | ±sn(z) | cn(z)/dn(z) | 負正sn(z) | |
1 | -dn(z)/(k*cn(z)) | ±1/(k*sn(z)) | dn(z)/(k*cn(z)) | 負正1/(k*sn(z)) | |
2 | -cn(z)/dn(z) | ±sn(z) | cn(z)/dn(z) | 負正sn(z) | |
2q | (-1)^p*sn(z) |
╲m n╲ | -1 | 0 | 1 | 2 | 2p |
-1 | -(ik')/(kcn(z)) | ±(idn(z))/(ksn(z)) | (ik')/(kcn(z)) | 負正(idn(z))/(ksn(z)) | |
0 | ±(k'sn(z))/dn(z) | cn(z) | 負正(k'sn(z))/dn(z) | -cn(z) | |
1 | (ik')/(kcn(z)) | 負正(idn(z))/(ksn(z)) | -(ik')/(kcn(z)) | ±(idn(z))/(ksn(z)) | |
2 | 負正(k'sn(z))/dn(z) | -cn(z) | ±(k'sn(z))/dn(z) | cn(z) | |
2q | (-1)^(p+q)*cn(z) |
╲m n╲ | -1 | 0 | 1 | 2 | p |
-1 | 負正(ik'sn(z))/cn(z) | ±(icn(z))/sn(z) | 負正(ik'sn(z))/cn(z) | ±(icn(z))/sn(z) | |
0 | k'/dn(z) | dn(z) | k'/dn(z) | dn(z) | |
1 | ±(ik'sn(z))/cn(z) | 負正(icn(z))/sn(z) | ±(ik'sn(z))/cn(z) | 負正(icn(z))/sn(z) | |
2 | -k'/dn(z) | -dn(z) | -k'/dn(z) | -dn(z) | |
q | (-1)^q*dn(z) |








加法定理



函式的平方之間的關係



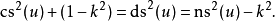
反函式


用Θ函式來定義


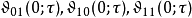




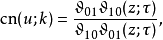

常微分方程的解[編輯]