基本介紹
- 中文名:模方程
- 外文名:modular equation
簡介
代數方程
模數
模空間
相關條目
- 拉馬努金遺失的筆記本
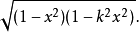
模方程(modular equation)是一個有模數的代數方程。給定一些在模空間中的函式,模方程是一些有關模空間函式的方程,或是一些有關模數的恆等式。...
中文名稱 混合模型方程組 英文名稱 mixed model equations;MME 定義 由亨德森(C.R. Henderson)於1953年推導的,以混合模型為基礎建立的線性方程組。對這種方程組...
模耦合是在光纖中各模間的功率交換現象。模耦合具有減少脈衝寬度展寬的有益效果。但亦需付出代價,因為任何使傳播模發生耦合的作用將同樣使傳播模同輻射模發生耦合,...
第一步,將上述Logistic模型方程(1)轉化為如下一個非線性方程(2)。第二步,方程(2)化簡轉化為如下方程(3)。第三步,方程(3)等式兩邊同時取對數轉化為如下方程...
Anderson(1979)率先在產品差異假設前提下推導出了引力方程,Bergstrand(1985,1989)則在簡單的壟斷競爭模型框架下利用貿易引力模型從理論上探討了決定雙邊貿易的因素,Help...
但實際上可以證明由等效控制方法所獲得的滑動模態方程是唯一的,並且在滿足一定的...第一部分是根據期望的系統動態特性進行滑模段的模面設計,以獲得滿意的控制性能;...
4、豐富的資料:Magma提供了非常豐富的示例和相關算法,它裡面包含了如對P^n+(-)1的因式分解,P是一個素數,模方程,強正則圖,極大子群的單群,積分格,K3的...
短期總需求—總供給模型方程為:AD=f (p) SAS=f(p)AD=SAS長期總需求—總供給模型方程為:AD=f (p) LAS=Y f AD=LAS= Yf...
模型方程為:V(dc/dt)=v(c0-c)c及c0分別為設備內及進口處示蹤物的濃度,t為時間,v為物料的體積流量,V為設備的工作體積。如將該模型方程用於連續流動設備,c...
(1)在傳統初始切線模量、極限偏應力的基礎上,引入“半值強度指數”的概念,建立了應力應變模型的數學特徵方程,分析了雙曲線應力應變模型數學特徵方程不獨立的缺陷。...
在1885年,亥維賽發表了第一篇關於描述他的電纜傳播分析和現代通信模式方程的論文。 [2] 傳輸線模型適用範圍 編輯 在許多電子線路中,連線各器件的電線的長度是...
1)描述車流的穩定性,由反應時間、靈敏度、前後兩車的車頭間距及前車速度等已知條件,列出跟車模型方程並求解,分析計算結果,根據跟隨車流的速度與車頭間距的變化...
其數學表達式則可以區分為微分方程、積分方程、代數方程、差分方程、微分-差分方程等。從描述水體的水體對象的不同,則可區分為河流水質模型、河口水質模型、湖泊(...
《大氣數值模式及模擬》系統講述大氣數值模式及其模擬的原理和方法。《大氣數值模式及模擬》的內容包括:大氣數值模式的基本概念;大氣數值模式設計的基本方程和動力框架;...
9.1耦合模方程9.2周期性波紋波導9.3布拉格反射濾波器9.4周期性波紋增益波導9.5分布反饋雷射器9.6雙波導定向耦合器9.7雙平板波導定向耦合器的耦合係數...
1)描述車流的穩定性,由反應時間、靈敏度、前後兩車的車頭間距及前車速度等已知條件,列出跟車模型方程並求解,分析計算結果,根據跟隨車流的速度與車頭間距的變化...
用適合於模式方程和計算區(有的適合邊界條件)的正交譜函式展開, 以求得和模式方程相當的以譜係數為未知數的方程的統稱。 套用學科 大氣科學(一級學科),動力氣象...
因而使代數數的理論獨立於代數基本定理;發現有理數域的任一阿貝爾擴張一定是一分圓域的子域,並提出著名猜想(見克羅內克青春之夢):橢圓函式具有複數乘法的模方程與...
以在大氣和下墊面(陸地、海面)上都達到能量平衡狀態作為約束條件而建立起來的簡化方程組。能量平衡模式有零維能量平衡模式,一維能量平衡模式,二維能量平衡模式等。...
5.9.1 耦合模方程5.9.2 縱向耦合特點5.10 單模光纖5.10.1 階躍型單模光纖5.10.2 梯度型單模光纖5.10.3 單模光纖的雙折射和偏振演化...
6.1.2 耦合模方程6.1.3 橢圓雙折射光纖6.2 非線性相移6.2.1 無色散交叉相位調製6.2.2 光克爾效應6.2.3 脈衝整形6.3 偏振態的演化...
