跟車模型反映的是跟隨車輛的駕駛員在獲得前導車的有關信息後所做出的刺激反應行為。駕駛員的刺激反應行為是指其為了跟蹤前車所作的加速或減速動作而做出的反應。影響駕駛員反應行為的因素較多，其中最主要的為前後車的速度差、前後車的距離、跟隨車的當前速度及其駕駛員的冒進程度等。
線性跟車模型建模的出發點是跟隨車保持與前車一定距離以避免前車剎車時與之相撞。雖然經典線性跟車模型考慮了後車駕駛員的感覺和反應時間，但車輛本身的動力特性的差異被忽略了。顯然易見，不同類型的車輛在不同車速狀態下，其最大的加速度與最大減速度是相異的。
基本介紹
- 中文名：線性跟車模型
- 外文名：linear car heel model
- 模型：描述刺激—反應問題
- 反映：跟隨車輛駕駛員做的刺激反應行為
- 穩定性：局部穩定性和漸變穩定
- 套用：描述車流的穩定性、行車安全等
模型的建立,模型的穩定性,跟車模型與車流模型,跟車理論的套用,
模型的建立
跟車模型是一種刺激—反應問題。一個司機所接受的刺激是指其前方導引車的加速或減速以及隨之而發生的這兩車之間的速度差和車間距離的變化；該司機對刺激的反應是指其為了緊密而又安全地跟蹤前車所作的加速或減速動作及其實際效果。
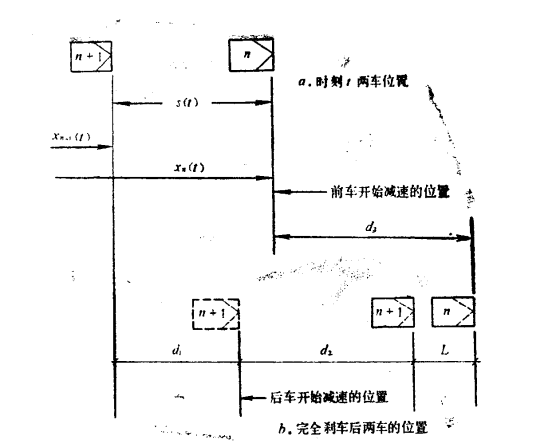
假定司機保持他所駕駛的車輛與前導車的距離為是s（t），以便在前導車剎車時能將車停下而不致於和前導車尾撞。設司機的反應時間為T，在反應時間內，車速不變。這兩輛車在t時刻的相對位置用下圖（a）表示，圖中n為前導車，n+1為後隨車。 兩車在剎車操作後的相對位置用圖（b）表示。圖中： ·
xi（t）——第i輛車在時刻t的位置；
s（t）——兩車在時刻t的間距=xn（t）-xn+1（t）；
d1——後隨車在反應時間T內行駛的距離=Tˊxn+1（t）=Tˊxn+1（t+T）；
d2——後隨車在減速期間行駛的距離；
d3——前導車在減速期間行駛的距離；
L——停車後的車頭間距；
xˊi（t）——第i輛車在時刻t的速度。
假定d2=d3，要使在時刻‘兩車的間距能保證在突然剎車事件中不發生撞碰，則應有
s（t）=d1+L=Tˊxn+1（t+T）+L
對t微分，得
xˊn（t）-xˊn+1（t）=Tˊˊxn+1（t+T）
模型或xˊˊn+1（t+T）=1/T[xˊn（t）-xˊn+1（t）] 式1
上式中：xˊˊn+1（t+T）為後車在時刻（t+T）的加速度，稱為後車的反應；1/T稱為敏感度；xˊn（t）-xˊn+1（t）稱為時刻t的刺激。這樣，式1就可理解為
反應=敏感度 × 刺激
式1是在前導車剎車、兩車的減速距離相等以及後車在反應時間r內速度不變等三條假定下推導出來的。實際的跟車操作要比這三條假定所限定的情形複雜得多。比方說，刺激也可能是由前車加速而引起的，而兩車在變速過程中行駛的距離可能不相等。為了適應更一般的情形，把式1修改為
xˊˊn+1（t+T）=α[xˊn（t）-xˊn+1（t）] 式2
式中：α稱為反應強度係數，量綱為秒-1。這裡α不應再理解為敏感度，而應看成是與司機動作的強弱程度直接相關。式2表明後車的反應與前車發出的刺激成正比，此公式稱為線性跟車模型。
模型的穩定性
在考察車輛跟駛特性時，一車隊車輛的穩定性問題是很重要的。這裡的所謂穩定性有兩個意思：一是指前後兩車的速度大致相等，車間距離大體保持某一常數值，這稱為局部穩定；另一是指某車的速度變化向其後各車傳播的特性，如速度變化的振幅在傳播中擴大了，叫做不穩定，如振幅逐漸衰減，則叫穩定。這種情形稱為漸近穩定。
上式是一個複雜的二階微分方程， 求解需剛拉普拉斯變換。海爾曼得出的結果是用c=αT取值的大小來表征穩定性。 這裡的α即為式中的反應強度係數，T為反應時間。海爾曼的結果如下：
（1）局部穩定性
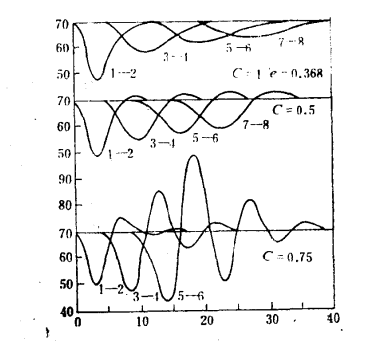
下表圖列出了不同的c值所對應的兩車間距的擺動情況。從中可以看出，隨著c值的增加，車間距逐漸地成為不穩定。這是由於，如果對早就出現的刺激（反應時間T長）反應太強烈（α大，表現在油門過大，或腳剎車踏得過重），使情況可能會偏向錯誤的方向。
c值與擺動情況對應表（2）漸近穩定
海爾曼的結果指山，一列行駛車輛儀當c<0.5時，才是漸近穩定的。帶頭車運行中的波動以α-1（秒/輛）的速率沿車隊向後傳播。當c>0.5時，將以增大波動幅度傳播，因而增大了車輛間的干擾，當干擾的幅度增加到使車頭間距小於一個車長時，則尾撞事故即將發生。
穩定性示意圖
穩定性示意圖右圖表示一列有8輛車的車隊在不同c值時的車頭間距。車輛間原來的間距為21米，當引導車減速後又加速至原來的速度時，圖上的曲線表示變動沿各車向後傳播的情形。
跟車模型與車流模型
車流模型是指在穩定的車流中，流量、車速和密度之間的相依關係。從跟車模型出發，可推導出各種車速—密度關係，方法是根據邊界條件解微分方程。
現用線性跟車模型推導車流模型。
積分式可得：
xˊn+1（t+T）=α[xn（t）-xn+1（t）]+c
車隊處於平穩狀態時，xˊn+1（t+T）=xˊn+1（t+），因此對任何t，上式都可化為
u =αs+c式3
令k =1/s，則k就是車流密度。利用邊界條許，可確定α和c。當u=0時，車隊的密度為擁塞密度ki，於是式3可寫成
u =α（1/k-1/ki） 式4
既然在跟車狀態下車輛的行駛是密度較高的非自由狀態，因此山線性跟車模型推導出來的車流模型式4，只適用於高密度情形。事實上，在式4中令眾k→0，則車速u趨向於無窮大，這是不合理的。向樣，在式中，流量在密度等於零寸達到最大值，也是不符合實際的。這是線性跟車模型的缺陷所在。
線性眼車模型的上述缺陷，究其根源在於它假定後隨車的跟駛反應只依賴刁：它與前導車的速度差，而與兩車的間距及後隨車本身的速度夫關。實際的情形表明，在一定的車速下，兩車的間距愈近，尾撞的潛在危險愈大，同時後隨車對前導車的速度變化的感知也愈快，因而反應愈加迅速和強烈。另一方面，後隨車本身的速度愈高，一旦發生尾撞的後果就愈嚴重，因而反應必須愈迅速和愈有效。
上式是跟車模型的最一般的形式，令參數m和I取各種不同的組合，積分後可導出各種不同的車流模型，其中包括歷史-亡不同研究者按其它不同方法提出的許多車流模型。下圖表列出了這些模型中常用的一部分。
對應於m，l不同組合的車流模型跟車理論的套用
2）依據跟車理論可尋求車輛跟車運動的規律，估計車流中前、後車之間的相互影響。為了維持與行車速度相適應的車頭間距，而不致過小，交通管理中可根據道路交通環境和氣候條件，控制車流量不超過規定的交通量，避免因流量過大，後車緊迫前車，形成追隨間隔縮小，造成一連串的尾撞事故的發生。在交通規劃與交通管理中，可以此作為依據進行流量分配，使路網交通量的分布，不超過規定的交通量數值。
3）依據跟車理論，在道路交通管理中設法使前車給後車駕駛員提供較多的信息，如提供車頭間距、相對速度等信息，以減少反應時間，幫助駕駛員跟隨車輛安全行駛，防止尾撞事故的發生。
4）通過計算機模擬車隊的跟車狀態，研究車輛跟車運行中的安全性。若能將道路交通系統中的駕駛員反應時間、車頭間距和相對速度的臨界值三個參數減至最少，便可增強駕駛員的感覺，縮短駕駛員反應的延滯時間，以減少交通事故。
5）通過跟車理論可分析公共汽車的腳踏車道流量。跟車試驗的穩定性分析表明：所有的數據點都在漸近穩定區內，且驗證了公共汽車跟車模型的預測；平均速度為53km/h，測出的公共汽車最大流量為1450veh/h。
通過跟車模型試驗可預測小型汽車，駛入市區環路、幹路的車流對市內交通的影響。
通過跟車模型試驗可預測小型汽車，駛入市區環路、幹路的車流對市內交通的影響。
6）由跟車模型的一般形式，當參數m和l取各種不同的組合時，經積分確定邊界條件，推導出各種不同的交通流模型。
