基本介紹
- 中文名:橢圓型偏微分方程
- 外文名:partial differential equation of elliptic type
- 代表:拉普拉斯方程
- 簡稱:橢圓型方程
定義


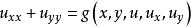


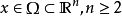





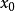
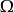
種類
線性
非線性
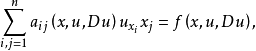

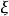
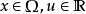
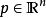





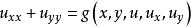


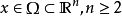





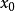
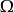
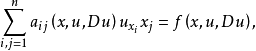

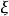
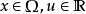
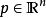


橢圓型偏微分方程,簡稱橢圓型方程,一類重要的偏微分方程。早在1900年D.希爾伯特提的著名的23個問題中,就有三個問題是關於橢圓型方程與變分法的。八十多年來,...
概念定義 (linear elliptic partial differential equations of second order)一 類關於自變數二一(二;,二:,…,二。)的未知函式u(二) 的二階線性偏微分方程 當...
6.2橢圓型方程組的高次可積性[1] 6.3變分極小點的正則性[1] 6.4調和映射的正則性[1] 習題6[1] 參考文獻[1] 參考資料 1. 橢圓型偏微分方程 .豆瓣網[...
1. 二階橢圓型偏微分方程 (第二版修訂版) .豆瓣[引用日期2017-04-13] 圖集 二階橢圓型偏微分方程圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:1次...
本書運用幾類具體的半線性橢圓型方程系統地介紹了反應擴散方程中的重要問題。主要內容包括:帶有擴散的兩物質自催化反應模型,帶有非單調反應函式的兩種群食餌-捕食...
包含未知函式的偏導數(或偏微分)的方程。方程中所出現未知函式偏導數的最高階數,稱為該方程的階。在數學、物理及工程技術中套用最廣泛的,是二階偏微分方程,習慣...
線性偏微分方程是一類重要的偏微分方程,關於所有未知函式及其導數都是線性的偏微分方程稱為線性偏微分方程。例如,拉普拉斯方程、熱傳導方程及波動方程都是線性偏微分...
二階擬線性橢圓型方程(quasilinear elliptic equations of second order)是關於二階導數為線性且其係數矩陣為正定的二階非線性偏微分方程,非線性偏微分方程是關於(...
偏微分方程特徵理論是偏微分方程論的一個基本概念。它對研究解的存在、唯一性及其他性質(例如奇性傳播)都有重要的意義。...
《橢圓型方程可解性研究》是合肥工業大學出版社2007年出版的圖書,作者是鐘金標,余桂東。 ...
混合型偏微分方程(partial differential equation of mixed type),簡稱混合型方程,一偏微分方程在所考慮的區域的某一部分上是橢圓型的,在另一部分上是雙曲型的,...
《偏微分方程基本理論》是2009年科學出版社出版的圖書,作者是王明新。...... 《偏微分方程基本理論》系統介紹了二階線性橢圓型方程、拋物型方程和雙曲型方程以及一...
《偏微分方程與數值方法》是2006年科學出版社出版的圖書,作者是拉松。...... 分別用三章闡述橢圓型、拋物型及雙曲型偏微分方程,一章關於其數學理論,一章關於其有...
《現代偏微分方程導論》是2007年10月1日科學出版社出版的圖書,作者是陳恕行。本書主要講述偏微分方程的一般理論、廣義函式與Sobolev空間、橢圓邊值問題、能量方法、...
本書是為高等院校計算數學專業高年級本科生和研究生偏微分方程數值解法課程編寫的教材。全書分為差分方法和有限元方法兩個相互獨立的部分。差分方法部分的先修課程...
物理學中的平衡態或定常態問題,例如彈性膜的平衡、彈性柱的扭轉、定常態熱傳導、電場、磁場、滲流、亞聲速流及不可壓縮無旋流等等,通常都可歸結為橢圓型偏微分...
