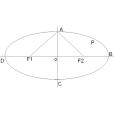
橢圓(橢圓形)

橢圓

橢圓形一般指本詞條

橢圓（Ellipse）是平面內到定點F1、F2的距離之和等於常數（大於|F1F2|）的動點P的軌跡，F1、F2稱為橢圓的兩個焦點。其數學表達式為：|PF1|+|PF2|=2a（2a>|F1F2|）。

橢圓是圓錐曲線的一種，即圓錐與平面的截線。

橢圓的周長等於特定的正弦曲線在一個周期內的長度。

基本介紹

  • 中文名：橢圓
  • 外文名：ellipse
  • 別名：橢圓形
  • 表達式：|PF1|+|PF2|=2a（2a>|F1F2|）
  • 適用領域：天文學
  • 套用學科：數學
  • 幾何類別：圓錐曲線
橢圓簡介,定義,第一定義,第二定義,其他定義,方程,標準方程,參數方程,極坐標,幾何性質,基本性質,切線法線,光學性質,相關公式,面積公式,周長,離心率,焦半徑,幾何關係,點與橢圓,直線與橢圓,套用,手工畫法,手繪法一,手繪法二,手繪法三,

橢圓簡介

在數學中，橢圓是圍繞兩個焦點的平面中的曲線，使得對於曲線上的每個點，到兩個焦點的距離之和是恆定的。因此，它是圓的概括，其是具有兩個焦點在相同位置處的特殊類型的橢圓。橢圓的形狀（如何“伸長”）由其偏心度表示，對於橢圓可以是從0（圓的極限情況）到任意接近但小於1的任何數字。
橢圓是封閉式圓錐截面：由錐體與平面相交的平面曲線。橢圓與其他兩種形式的圓錐截面有很多相似之處：拋物線和雙曲線，兩者都是開放的和無界的。圓柱體的橫截面為橢圓形，除非該截面垂直於圓柱體軸線。
橢圓也可以被定義為一組點，使得曲線上的每個點的距離與給定點（稱為焦點）的距離與曲線上的相同點的距離的比值給定行（稱為directrix）是一個常數。該比率稱為橢圓的偏心率。
也可以這樣定義橢圓，橢圓是點的集合，點其到兩個焦點的距離的和是固定數。
橢圓在物理，天文和工程方面很常見。

定義

第一定義

平面內與兩定點
、
的距離的和等於常數
（
）的動點P的軌跡叫做橢圓。
即：
其中兩定點
、
叫做橢圓的焦點，兩焦點的距離
叫做橢圓的焦距。
為橢圓的動點。
橢圓截與兩焦點連線重合的直線所得的弦為長軸，長為
。
橢圓截垂直平分兩焦點連線的直線所得弦為短軸，長為
。
可變為
。
橢圓
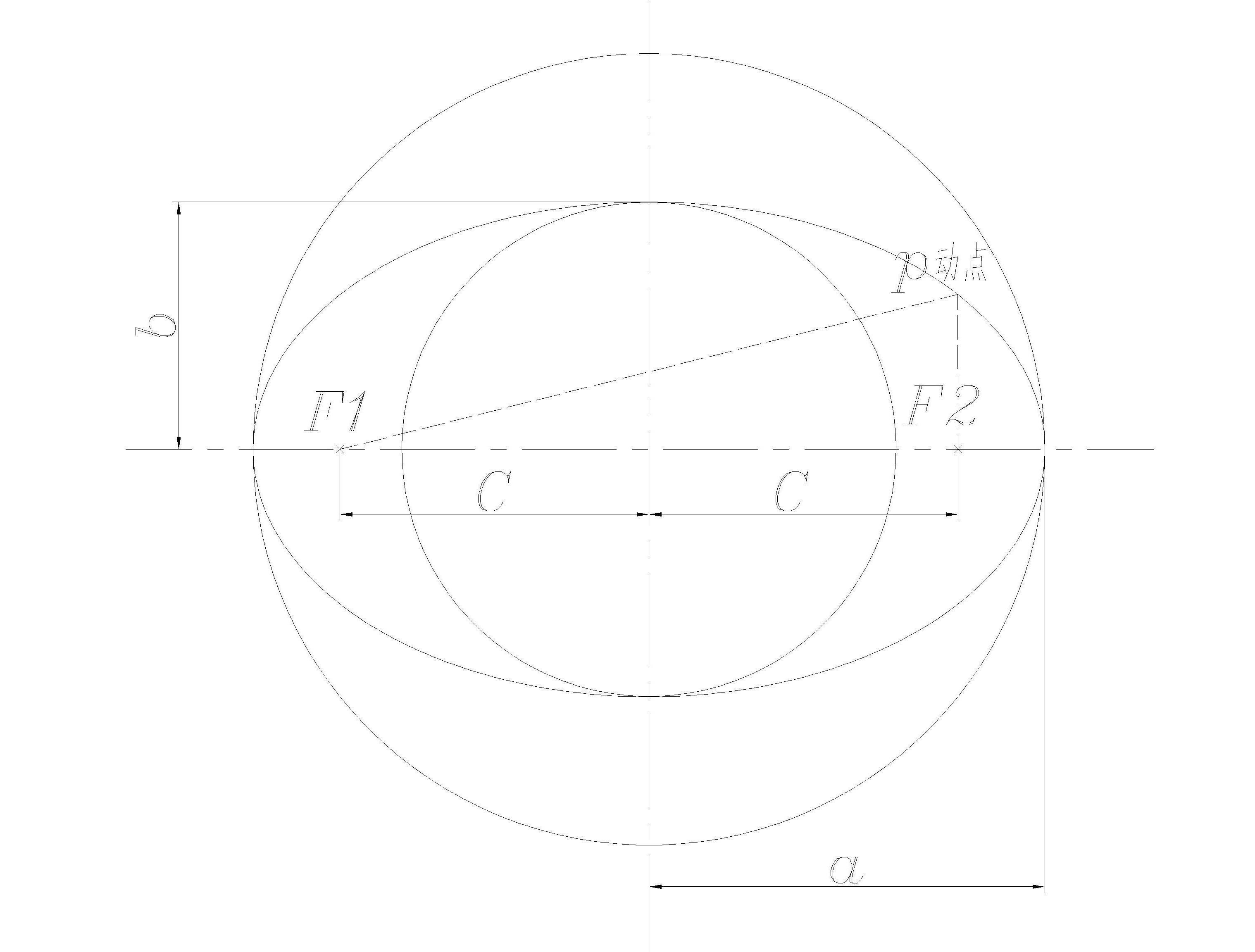
橢圓定義說明
橢圓
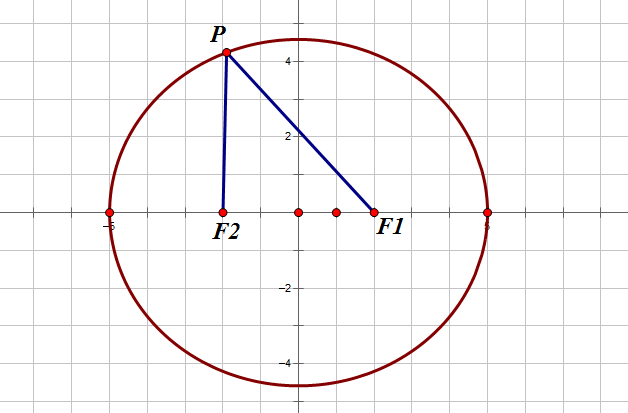
橢圓定義

第二定義

橢圓平面內到定點
（c，0）的距離和到定直線
：
（
不在
上）的距離之比為常數
（即離心率
，0<e<1）的點的軌跡是橢圓。
其中定點
為橢圓的焦點，定直線
稱為橢圓的準線〈該定直線的方程是
（焦點在x軸上），或
（焦點在y軸上）〉。

其他定義

根據橢圓的一條重要性質：橢圓上的點與橢圓長軸（事實上只要是直徑都可以）兩端點連線的斜率之積是定值，定值為
〈前提是長軸平行於x軸。若長軸平行於y軸，比如焦點在y軸上的橢圓，可以得到斜率之積為 -a/b=1/（e-1）〉，可以得出：
在坐標軸內，動點（
）到兩定點（
）（
）的斜率乘積等於常數m（-1<m<0）。
注意：考慮到斜率不存在時不滿足乘積為常數，所以
無法取到，即該定義僅為去掉四個點的橢圓。
橢圓也可看做圓按一定方向作壓縮或拉伸一定比例所得圖形。

方程

標準方程

在平面直角坐標系中，用方程描述了橢圓，橢圓的標準方程中的“標準”指的是中心在原點，對稱軸為坐標軸。
橢圓
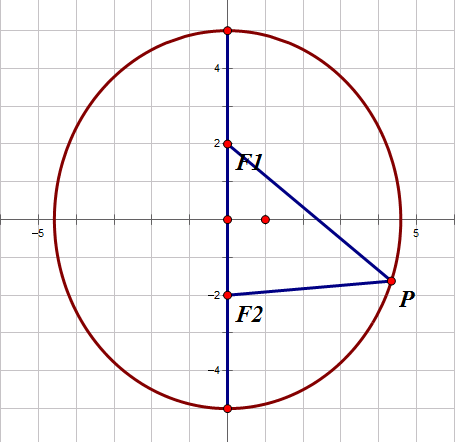
橢圓定義
橢圓的標準方程有兩種，取決於焦點所在的坐標軸：
1.焦點在X軸時，標準方程為：
2.焦點在Y軸時，標準方程為：
橢圓上任意一點到F1，F2距離的和為2a，F1，F2之間的距離為2c。而公式中的b=a-c。b是為了書寫方便設定的參數。
又及：如果中心在原點，但焦點的位置不明確在X軸或Y軸時，方程可設為mx+ny=1（m>0，n>0，m≠n）。即標準方程的統一形式。
橢圓的面積是πab。橢圓可以看作圓在某方向上的拉伸，它的參數方程是：x=acosθ ， y=bsinθ
標準形式的橢圓在（x0，y0）點的切線就是 ：xx0/a+yy0/b=1。橢圓切線的斜率是：-bx0/ay0，這個可以通過複雜的代數計算得到。
橢圓(橢圓形)
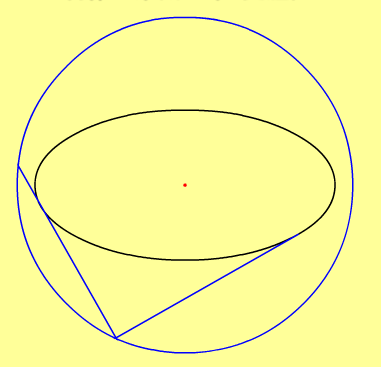
點與橢圓

參數方程

x=acosθ ， y=bsinθ。
求解橢圓上點到定點或到定直線距離的最值時，用參數坐標可將問題轉化為三角函式問題求解
x=a×cosβ， y=b×sinβ a為長軸長的一半 b為短軸長的一半

極坐標

（一個焦點在極坐標系原點，另一個在θ=0的正方向上）
（e為橢圓的離心率=c/a）。

幾何性質

基本性質

1、範圍：焦點在
軸上
，
；焦點在
軸上
，
。
2、對稱性：關於X軸對稱，Y軸對稱，關於原點中心對稱。
3、頂點：（a，0）（-a，0）（0，b）（0，-b）。
4、離心率：
或 e=√（1-b^2/a）。
5、離心率範圍：0<e<1。
6、離心率越小越接近於圓，越大則橢圓就越扁。
7、焦點（當中心為原點時）：（-c，0），（c，0）或（0，c），（0，-c）。
8、
與
（m為實數）為離心率相同的橢圓。
9、P為橢圓上的一點，a-c≤PF1（或PF2）≤a+c。
10、橢圓的周長等於特定的正弦曲線在一個周期內的長度。

切線法線

定理1：設F1、F2為橢圓C的兩個焦點，P為C上任意一點。若直線AB切橢圓C於點P，且A和B在直線上位於P的兩側，則∠APF1=∠BPF2。（也就是說，橢圓在點P處的切線即為∠F1PF2的外角平分線所在的直線）。
定理2：設F1、F2為橢圓C的兩個焦點，P為C上任意一點。若直線AB為C在P點的法線，則AB平分∠F1PF2。
上述兩定理的證明可以查看參考資料。
解析幾何法求證橢圓切線定理：
解：設C：（（x^2）/（a^2））+（（y^2）/（b^2））=1-----式1；
（a^2）-（b^2）=（c^2）；
F1（-c，0）；F2（c，0）；P（xp，yp）
AB：（y-yp）=k（x-xp）=>y=kx+（yp-kxp）；令m=yp-kxp=>AB：y=kx+m-----式2；
聯立式1和式2消去y得：（（k^2）+（（b^2）/（a^2）））（x^2）+2kmx+（（m^2）-（b^2））=0；
因為直線AB切橢圓C於點P，所以上式只有唯一解，則：
4（（km）^2）-4（（k^2）+（（b^2）/（a^2）））（（m^2）-（b^2））=0=>m^2=（（ak）^2）+（b^2）；
m^2=（yp-kxp）^2=（（yp）^2）+（（kxp）^2）-2kxpyp=（（ak）^2）+（b^2）；
=>（（a^2）-（xp^2））（k^2）+2xpypk+（（b^2）-（yp^2））；
由根的判別式得：4（（xpyp）^2）-4（（a^2）-（xp^2））（（b^2）-（yp^2））=0；
所以k值有唯一解：k=（-2xpyp）/（2（（a^2）-（xp^2）））=-xpyp/（（a^2）-（xp^2））；
由式1得：（a^2）-（xp^2）=（ayp/b）^2=>k=-（xp（b^2））/（yp（a^2））；
m=yp-kxp=（（（ypa）^2）+（（xpb）^2））/（yp（a^2））=（（ab）^2）/（yp（a^2））=（b^2）/yp；
設A0F1、B0F2分別過F1、F2垂直AB於A0、B0；
A0F1：（y-0）=（-1/k）（x+c）=>x+ky+c=0-----式3；
聯立式2和式3消去y得：x=-（km+c）/（（k^2）+1）；
聯立式2和式3消去x得：y= （m-kc）/（（k^2）+1）；
則：A0：（-（km+c）/（（k^2）+1），（m-kc）/（（k^2）+1））；
|A0F1|^2=（（m-kc）^2）/（（k^2）+1））；
同理：B0F2：（y-0）=（-1/k）（x-c）；
=>B0：（（c-km）/（（k^2）+1），（m+kc）/（（k^2）+1））；
|B0F2|^2=（（m+kc）^2）/（（k^2）+1））；
|PF1|^2=（（xp+c）^2）+（yp^2）；
|PF2|^2=（（xp-c）^2）+（yp^2）；
證明：若∠APF1=∠BPF2，則直角三角形A0PF1與直角三角形B0PF2相似；
=>|A0F1|/|PF1|=|B0F2|/|PF2|
=>（|A0F1|^2）/（|PF1|^2）=（|B0F2|^2）/（|PF2|^2）
=>（|PF2|^2）/（|PF1|^2）=（|B0F2|^2）/（|A0F1|^2）
（（m+kc）^2）/（（m-kc）^2）=（（（xp-c）^2）+（yp^2））/（（（xp+c）^2）+（yp^2））；-----式4
m+kc=（b^2）/yp-（xpc（b^2））/（yp（a^2））=（（a^2）-xpc）（b^2）/（yp（a^2））；-----式5
m-kc=（b^2）/yp+（xpc（b^2））/（yp（a^2））=（（a^2）+xpc）（b^2）/（yp（a^2））；----式6
把式5和式6代入式4得：
（（（a^2）-xpc）^2）/（（（a^2）+xpc）^2）=（（（xp-c）^2）+（yp^2））/（（（xp+c）^2）+（yp^2））；
=>（（（a^2）-xpc）^2）（（（xp+c）^2）+（yp^2））=（（（a^2）+xpc）^2）（（（xp-c）^2）+（yp^2））
=>（（（a^2）-xpc）^2）（（xp+c）^2）+（（（a^2）-xpc）^2）（yp^2）=（（（a^2）+xpc）^2）（（xp-c）^2）+（（（a^2）+xpc）^2）（yp^2）
=>[（（（a^2）-xpc）^2）（（xp+c）^2）-（（（a^2）+xpc）^2）（（xp-c）^2）]=[（（（a^2）+xpc）^2）-（（（a^2）-xpc）^2）]（yp^2）
=>[（（a^2）-xpc）（xp+c）+（（a^2）+xpc）（xp-c）][（（a^2）-xpc）（xp+c）-（（a^2）+xpc）（xp-c）]=4xpc（ayp）^2
=>（2（a^2）xp-2（c^2）xp）（2c（a^2）-2c（xp^2））=4xpc（ayp）^2
=>4xpc（b^2）（（a^2）-（xp^2））=4xpc（ayp）^2
=>（b^2）（（a^2）-（xp^2））=（ayp）^2
=>（ab）^2=（（ayp）^2）+（（bxp）^2）
=>（（xp^2）/（a^2））+（（yp^2）/（b^2））=1等式成立，∠APF1=∠BPF2得證。

光學性質

橢圓的面鏡（以橢圓的長軸為軸，把橢圓轉動180度形成的立體圖形，其內表面全部做成反射面，中空）可以將某個焦點發出的光線全部反射到另一個焦點處；橢圓的透鏡（某些截面為橢圓）有匯聚光線的作用（也叫凸透鏡），老花眼鏡、放大鏡和遠視眼鏡都是這種鏡片（這些光學性質可以通過反證法證明）。

相關公式

面積公式

（其中
分別是橢圓的長半軸、短半軸的長），或
（其中
分別是橢圓的長軸，短軸的長）。
證：
的面積，由於圖形的對稱性可知，只要求出第一象限的面積乘以4即可。
在第一象限
， 令

周長

橢圓周長計算公式：L=T（r+R）
T為橢圓係數，可以由r/R的值，查表找出係數T值；r為橢圓短半徑；R為橢圓長半徑。
橢圓周長定理：橢圓的周長等於該橢圓短半徑與長半徑之和與該橢圓係數的積（包括正圓）。
附橢圓係數簡表：
橢圓係數簡表
r / R
係數
r / R
係數
r / R
係數
r / R
係數
0.01
3.961483495
0.26
3.418920439
0.51
3.224856225
0.76
3.156214217
0.02
3.925332509
0.27
3.40695685
0.52
3.220415735
0.77
3.154868403
0.03
3.891174223
0.28
3.395457698
0.53
3.216154903
0.78
3.153601776
0.04
3.858791647
0.29
3.384403803
0.54
3.212067616
0.79
3.152411903
0.05
3.828024399
0.3
3.373776976
0.55
3.208148
0.8
3.151296432
0.06
3.798743616
0.31
3.363559954
0.56
3.204390411
0.81
3.150253089
0.07
3.770841059
0.32
3.353736335
0.57
3.200789422
0.82
3.149279677
0.08
3.744223265
0.33
3.344290532
0.58
3.197339815
0.83
3.148374067
0.09
3.718808013
0.34
3.335207712
0.59
3.194036571
0.84
3.147534204
0.1
3.694521982
0.35
3.326473758
0.6
3.190874858
0.85
3.146758097
0.11
3.671299121
0.36
3.318075219
0.61
3.187850029
0.86
3.146043822
0.12
3.649079455
0.37
3.309999276
0.62
3.184957608
0.87
3.145389514
0.13
3.627808177
0.38
3.302233702
0.63
3.182193286
0.88
3.144793371
0.14
3.607434941
0.39
3.294766828
0.64
3.179552911
0.89
3.144253646
0.15
3.587913299
0.4
3.287587514
0.65
3.177032484
0.9
3.143768649
0.16
3.569200238
0.41
3.280685115
0.66
3.174628151
0.91
3.143336742
0.17
3.551255799
0.42
3.274049459
0.67
3.172336195
0.92
3.14295634
0.18
3.534042762
0.43
3.267670819
0.68
3.170153034
0.93
3.142625907
0.19
3.517526368
0.44
3.261539886
0.69
3.168075214
0.94
3.142343956
0.2
3.50167409
0.45
3.255647754
0.7
3.166099401
0.95
3.142109044
0.21
3.486455429
0.46
3.249985893
0.71
3.164222379
0.96
3.141919775
0.22
3.471841741
0.47
3.244546132
0.72
3.162441046
0.97
3.141774794
0.23
3.457806077
0.48
3.239320639
0.73
3.160752407
0.98
3.141672788
0.24
3.444323049
0.49
3.234301909
0.74
3.159153568
0.99
3.141612486
0.25
3.43136871
0.5
3.22948274
0.75
3.157641737
1
π
工程運用橢圓係數簡表
r / R
係數
r / R
係數
r / R
係數
r / R
係數
1
π
0.4787
3.24
0.2011
3.5
0.0739
3.76
0.9555
3.142
0.4599
3.25
0.1946
3.51
0.0703
3.77
0.9188
3.143
0.4422
3.26
0.1884
3.52
0.0666
3.78
0.8951
3.144
0.4263
3.27
0.1824
3.53
0.0631
3.79
0.8764
3.145
0.4111
3.28
0.1764
3.54
0.0595
3.8
0.8607
3.146
0.3966
3.29
0.1707
3.55
0.0561
3.81
0.8468
3.147
0.3829
3.3
0.1651
3.56
0.0526
3.82
0.8433
3.148
0.3699
3.31
0.1595
3.57
0.0493
3.83
0.8231
3.149
0.3577
3.32
0.1541
3.58
0.0461
3.84
0.8126
3.15
0.3459
3.33
0.1489
3.59
0.0428
3.85
0.7689
3.155
0.3414
3.34
0.1437
3.6
0.0396
3.86
0.7347
3.16
0.3239
3.35
0.1387
3.61
0.0364
3.87
0.7058
3.165
0.3136
3.36
0.1337
3.62
0.0333
3.88
0.6806
3.17
0.3036
3.37
0.1289
3.63
0.0303
3.89
0.6584
3.175
0.2941
3.38
0.1242
3.64
0.0273
3.9
0.6383
3.18
0.2848
3.39
0.1195
3.65
0.0244
3.91
0.6199
3.185
0.2759
3.4
0.1149
3.66
0.0215
3.92
0.6028
3.19
0.2674
3.41
0.1105
3.67
0.0186
3.93
0.5871
3.195
0.2591
3.42
0.1062
3.68
0.0158
3.94
0.5722
3.2
0.2511
3.43
0.1019
3.69
0.0131
3.95
0.5583
3.205
0.2432
3.44
0.0977
3.7
0.0103
3.96
0.5452
3.21
0.2357
3.45
0.0935
3.71
0.0077
3.97
0.5328
3.215
0.2284
3.46
0.0895
3.72
0.0051
3.98
0.5097
3.225
0.2212
3.47
0.0855
3.73
0.0025
3.99
0.4989
3.23
0.2143
3.48
0.0816
3.74
0.0012
3.995
0.4886
3.235
0.2076
3.49
0.0777
3.75
0.0002
3.999
橢圓與三角函式的關係
關於橢圓的周長等於特定的正弦曲線在一個周期內的長度的證明：
半徑為r的圓柱上與一斜平面相交得到一橢圓，該斜平面與水平面的夾角為α，截取一個過橢圓短徑的圓。以該圓和橢圓的某一交點為起始轉過一個θ角。則橢圓上的點與圓上垂直對應的點的高度可以得到f（c）=r tanα sin（c/r）。
r：圓柱半徑；
α：橢圓所在面與水平面的角度；
c：對應的弧長（從某一個交點起往某一個方向移動）；
以上為證明簡要過程，則橢圓（x*cosα）^2+y^2=r^2的周長與f（c）=r tanα sin（c/r）的正弦曲線在一個周期內的長度是相等的，而一個周期T=2πr，正好為一個圓的周長。

離心率

橢圓離心率的定義為橢圓上焦距與長軸的比值，（範圍：0<X<1）。
e=c/a（0<e<1），因為2a>2c。離心率越大，橢圓越扁平；離心率越小，橢圓越接近於圓形。
橢圓的焦準距：橢圓的焦點與其相應準線（如焦點（c，0）與準線x=±a^2/c） 的距離為a^2/c-c=b^2/c
離心率與
的關係：
。

焦半徑

焦點在x軸上：|PF1|=a+ex |PF2|=a-ex（F1，F2分別為左右焦點）。
橢圓過右焦點的半徑r=a-ex。
過左焦點的半徑r=a+ex。
焦點在y軸上：|PF1|=a+ey |PF2|=a-ey（F2，F1分別為上下焦點）。
橢圓的通徑：過焦點的垂直於x軸（或y軸）的直線與橢圓的兩交點A，B之間的距離，即|AB|=2*b^2/a。

幾何關係

點與橢圓

點M（x0，y0）橢圓 x^2/a^2+y^2/b^2=1；
點在圓內：x0/a+y0/b<1；
點在圓上：x0/a+y0/b=1；
點在圓外：x0/a+y0/b>1；
跟圓與直線的位置關係一樣的：相交、相離、相切。
橢圓(橢圓形)
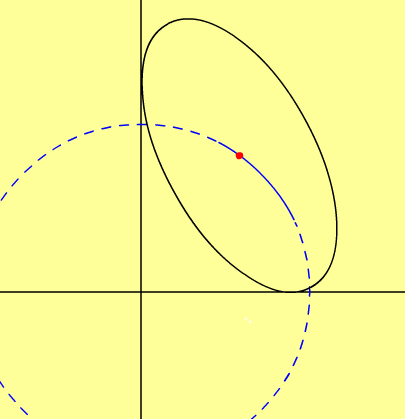
直線與橢圓

直線與橢圓

y=kx+m ①
x/a+y/b=1 ②
由①②可推出xa+（kx+m）/b=1
相切△=0
相離△<0無交點
相交△>0 可利用弦長公式：設A（x1，y1） B（x2，y2）
求中點坐標
根據韋達定理 x1+x2=-b/a，x1x2=c/a
代入直線方程可求出 （y1+y2）/2=可求出中點坐標。
|AB|=d = √（1+k）[（x1+x2）-4x1*x2] = √（1+1/k）[（y1+y2）-4y1y2]
橢圓(橢圓形)
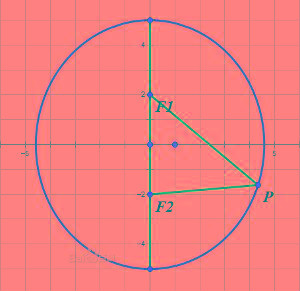
橢圓

套用

例如：有一個圓柱，被截得到一個截面，下面證明它是一個橢圓（用上面的第一定義）：
將兩個半徑與圓柱半徑相等的半球從圓柱兩端向中間擠壓，它們碰到截面的時候停止，那么會得到兩個公共點，顯然他們是截面與球的切點。
設兩點為F1、F2
對於截面上任意一點P，過P做圓柱的母線Q1、Q2，與球、圓柱相切的大圓分別交於Q1、Q2
則PF1=PQ1、PF2=PQ2，所以PF1+PF2=Q1Q2
由定義1知：截面是一個橢圓，且以F1、F2為焦點
橢圓(橢圓形)
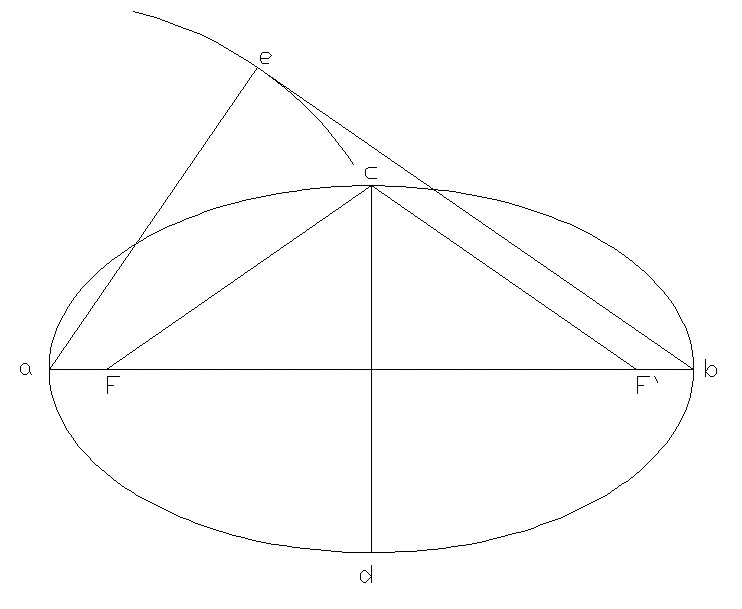
已知長軸與短軸尺寸，兩焦點焦距尺規作圖法
用同樣的方法，也可以證明圓錐的斜截面（不通過底面）為一個橢圓
例：已知橢圓C：x^2/a^2+y^2/b^2=1（a>b>0）的離心率為√6/3，短軸一個端點到右焦點的距離為√3.
1．求橢圓C的方程.
2．直線l：y=x+1與橢圓交於A，B兩點，P為橢圓上一點，求△PAB面積的最大值.
3．在⑵的基礎上求△AOB的面積.
一 分析短軸的端點到左右焦點的距離和為2a，端點到左右焦點的距離相等（橢圓的定義），可知a=√3，又c/a=√6/3，代入得c=√2，b=√（a^2-c^2）=1，方程是x^2/3+y^2/1=1，
二 要求面積，顯然以ab作為三角形的底邊，聯立x^2/3+y^2/1=1，y=x+1解得x1=0，y1=1，x2=-1.5，y2=-0.5.利用弦長公式有√（1+k^2））[x2-x1]（中括弧表示絕對值）弦長=3√2/2，對於p點面積最大，它到弦的距離應最大，假設已經找到p到弦的距離最大，過p做弦的平行線，可以 發現這個平行線是橢圓的切線是才會最大，這個切線和弦平行故斜率和弦的斜率=，設y=x+m，利用判別式等於0，求得m=2，-2.結合圖形得m=-2.x=1.5，y=-0.5，p（1.5，-0.5），
三 直線方程x-y+1=0，利用點到直線的距離公式求得√2/2，面積1/2*√2/2*3√2/2=3/4，

手工畫法

手繪法一

（1）：畫長軸AB，短軸CD，AB和CD互垂平分於O點。
（2）：連線AC。
（3）：以O為圓心，OA為半徑作圓弧交OC延長線於E點。
（4）：以C為圓心，CE為半徑作圓弧與AC交於F點。
（5）：作AF的垂直平分線交CD延長線於G點，交AB於H點。
（6）：截取H，G對於O點的對稱點H’，G’ ⑺：H，H’為長軸圓心，分別以HA、H‘B為半徑作圓；G，G’為短軸圓心，分別以GC、G‘D為半徑作圓。
用一根線或者細銅絲，鉛筆，2個圖釘或大頭針畫橢圓的方法：先畫好長短軸的十字線，在長軸上以圓點為中心先找2個大於短軸半徑的點，一個點先用圖釘或者大頭針栓好線固定住，另一個點的線先不要固定，用筆帶住線去找長短軸的4個頂點，此步驟需要多次定位，直到都正好能於頂點吻合後固定住這2個點，用筆帶住線，直接畫出橢圓：）使用細銅絲最好，因為線的彈性較大畫出來不一定準確。

手繪法二

橢圓的焦距│FF'│（Z）定義，為已知橢圓所構成的長軸X（ab）與短軸Y（cd）則以長軸一端A為圓心短軸Y為半徑畫弧，從長軸另一段點B引出與弧相切的線段則為該橢圓焦距，求證公式為2√{（Z/2）^2+（Y/2）^2}+Z=X+Z（平面內與兩定點F、F'的距離的和等於常數2a（2a>|FF'|）的動點P的軌跡叫做橢圓），可演變為z=√x^2-y^2（x>y>0）。Z兩端點F、F'為定點。取有韌性且伸縮係數越小越好的線，環繞線段AF'或者FB線段任意一組為長度，以該長度為固定三角形周長，以F、F'　為定點、取構成該三角形上的第三點為動點畫弧則構成該橢圓。
橢圓(橢圓形)
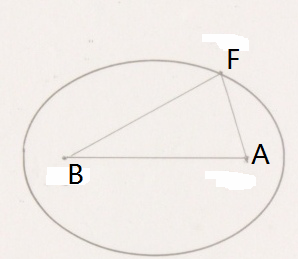
橢圓示意圖

手繪法三

環線長
。根據橢圓的圖形特徵，採用環線表示動點與焦點間的距離關係，形成統一的圓形環線作圖法。具體方法簡介：
（1）作圖工具為筆、大頭針、直尺和環形線。（環形線製作：取一段長度（30—50cm）和粗細適中彈性小的軟線、一段8mm長細電線空塑膠管，軟線從塑膠管中相向竄過，塑膠管將軟線夾緊，但用力可以抽動，形成能收縮和放長的環形線）。
（2）在作圖平面上作出各種圓形的定點和動點。
（3）將大頭針分別直立、固定在定點上；
（4）將符合長度的環形線套在大頭針外，畫筆由內向外拉直環線，通過調整環線的長度使筆尖剛好落在動點上；
（5）將畫筆移動一周，即可作出各種圓的圖形。
環線作圖方法的最大特點，就是把圓形的動點與焦點間的距離關係以環線的方式聯繫起來，而不受焦點數目的影響，環線內可以容納任意焦點數目，為探討3個及其3個以上焦點數目的多焦點圓提供有效方法。環線作圖方法，屬於連續移動作圖法，適合不同大小的圓、橢圓和卵圓等作圖。
若用該方法畫規定半長軸a和半短軸b的橢圓，則
，環線長

相關詞條

熱門詞條

聯絡我們