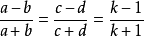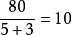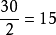解釋
簡介
比例是一個總體中各個部分的數量占總體數量的比重,用於反映總體的構成或者結構。
比例分為比例尺和比例兩種.表示兩個比相等的式子叫做比例。判斷兩個比能不能組成比例,要看它們的比值是不是相等。組成比例的四個數,叫做比例的項。兩端的兩項叫做比例的外項,中間的兩項叫做比例的內項。在比例里,兩個外項的積等於兩個內項的積,這是
比例的基本性質。求比例其中一個未知項,叫做
解比例。
舉例說明
①表示兩個比值相等的式子叫做比例,如3:4=9:12、7:9=21:27
比例有四個項,分別是兩個內項和兩個外項;在7:9=21:27中,其中7與27叫做比例的外項,9與21叫做比例的內項。
②比如:教師和學生的~已經達到要求。
④比例寫成分數的形式後,那么,左邊的分母和右邊的分子是內項;左邊的分子和右邊的分母是外項。
⑤比例的基本性質:在一個比例中,兩個外項的積等於兩個內項的積。
正比例與反比例
正比例
兩種相關聯的量,一種量變化,另一種量也隨著變化,如果兩種量中相對應的兩個數的比值(商)一定,這兩種量就叫做成正比例的量,他們的關係叫做正比例關係。如果用
字母x和y表示兩種關聯的量,用k表示它們的比值,成
正比例關係可以用下面式子表示:y/x=k(一定)
反比例
兩種相關聯的量,一種量變化,另一種量也隨著變化,如果兩種量中相對應的兩個數的乘積一定,這兩種量就叫做成反比例的量,他們的關係叫做
反比例關係。如果用字母x和y表示兩種關聯的量,用k表示它們的乘積,成反比例關係可以用下面式子表示:xy=k(一定)
反比例性的概念可以與直接相稱性進行對比。考慮兩個變數被認為是“相互成比例”的。如果所有其他變數保持不變,如果另一個變數增加,則一個反比例變數的幅度或絕對值減小,而其乘積(比例常數k)總是相同的。
如果每個變數與另一個變數的乘數相反(倒數)成正比,則兩個變數成反比(也稱為反向變化,反向變異,反比例),如果其乘積是一個常數。因此,如果存在非零常數k,則變數y與變數x成反比:
例如,旅途所需的時間與旅行速度成反比;挖洞所需的時間(大概)與挖掘人數成反比。
在笛卡爾坐標平面上反向變化的兩個變數的曲線圖是矩形雙曲線。曲線上每個點的x和y值的乘積等於比例常數(k)。既然x和y都不能等於零(因為k是非零),所以圖形從不跨任一個軸。
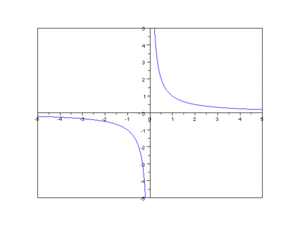 反比例函式
反比例函式如何判斷
在解決此類問題過程中要緊緊抓住正反比例的意義,一是看不是兩種相關聯的量,二看這兩個量之間的商一定還是積一定的。商一定,兩個量
成正比例;積一定,兩個量成反比例。其次在解決實踐套用問題時要注意比和比例,以及它們和分數之間的關係。然後再綜合所學過的知識進行解答。
比與比例的區別
比表示兩個數相除(有兩項,前項和後項),比例表示兩個比相等的式子(有四項,兩個內項,兩個外項)。
解比例
比例分為
比例尺和比例.表示兩個比相等的式子叫做比例。判斷兩個比能不能組成比例,要看它們的比值是不是相等。
在比例里,兩個外項的積等於兩個內項的積。已知比例中的任何三項,就可以求出這個比例中的另外一個未知項。求比例中的未知項,叫做
解比例。 解比例都是運用比例的基本性質來解的,因為兩外項的積等於兩內項的積,所以我們可以把兩個外項和內項互相乘起來,再來解這個
方程。比如:x:3= 9:27
解法:
x:3=9:27
解:27x=3×9
27x=27
x=1
比例具有如下性質:
若a:b=c:d(b.d≠0),則有
1) ad=bc (即比例的基本性質:兩個外項的積等於兩個內項的積)
2) b:a=d:c (a.c≠0) (交換比較,結果仍然相等)
3) a:c=b:d ; c:a=d:b
4) (a+b):b=(c+d):d
5) a:(a+b)=c:(c+d) ( a+b≠0,c+d≠0)
6) (a-b):(a+b)=(c-d):(c+d) ( a+b≠0,c+d≠0)
證明過程如下
令 a:b=c:d=k,
∵a:b=c:d
∴a=bk;c=dk
1)∴ad=bk*d=kbd;bc=b*dk=kbd
∴ad=bc
2) 顯然b:a=d:c=1/k
3) a:c=bk:dk=b:d ;結合性質2有c:a=d:b
4) ∵a:b=c:d
∴(a/b)+1=(c/d)+1
∴(a+b)/b=(c+d)/d=1+k ;即 (a+b):b=(c+d):d
a+b≠0,c+d≠0時,結合性質2有b:(a+b)=d:(c+d)
5) ∵b/(a+b)=d/(c+d)
∴1- b/(a+b)=1- d/(c+d)=1-1/(k+1)
∴a/(a+b)=c/(c+d)=k/k+1 ……②
即a:(a+b)=c:(c+d)
a+b≠0,c+d≠0時,結合性質2有 (a+b):a=(c+d):c
7) 做做此題:一個長方形,比為5:3,長方形的周長是80米,求它的長和寬。
(有意者,請做在後面。)
假設長方形長為5X,寬為3X,那么:
(5X+3X)*2=80
8X=40
X=5
長:5X=5*5=25(米) 寬:3X=5*3=15(米)
答:這個長方形的長是25米,寬是15米。
或:
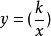

 反比例函式
反比例函式