基本介紹
- 中文名:機率賦范線性空間
- 外文名:proba bilistic normed line-ar space
- 適用範圍:數理科學
簡介
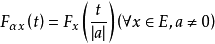
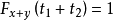
推廣
機率度量空間
賦范線性空間







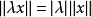



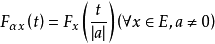
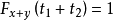







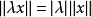



機率賦范線性空間是賦范線性空間的概念到機率度量空間情形的推廣。...... 機率賦范線性空間是賦范線性空間的概念到機率度量空間情形的推廣。設E是實線性空間,𝒟為...
機率賦范空間(probabilistic normed space)簡稱賦范空間,是賦范空間概念的一種推廣,是由塞斯特內夫( A.N.Šerstnev)在1962年引入的,機率賦范空間為機率度量空間...
賦范線性空間(normed linear space)是線上性空間中引進一種與代數運算相聯繫的度量,即由向量範數誘導出的度量。賦范線性空間稱為Banach空間,是指由範數導出的度量...
則稱 為機率線性賦范度量空間,記為PN空間。注意:令 ,易得機率線性賦范度量空間為機率度量空間的特例。[1] 機率度量空間M-PM空間 ...
嚴格凸賦范線性空間(strictly convex normed linear space)是滿足嚴格凸性的一類賦范線性空間,簡稱為嚴格凸空間,常用於討論最佳逼近元的唯一性,以及有界線性泛函保...
平性凸賦范線性空間(flat convex normed linear space)是一類賦范線性空間。...... 平性凸賦范線性空間(flat convex normed linear space)是一類賦范線性空間。...
賦范線性空間是一類可以引進“長度”概念的線性空間。 一致凸賦范線性空間(uniformly convexnormed linear space)是滿足一致凸性的一類賦范線性空間。 [1] 中文...
商賦范線性空間是由賦范線性空間與其閉子空間誘導出的新的賦范線性空間。...... 商賦范線性空間是由賦范線性空間與其閉子空間誘導出的新的賦范線性空間。...
設{X(t),t∈R+}為定義在機率空間(Ω,F,P)上取值於可測空間(E,E)的...完備的賦范線性空間被稱為巴拿赫空間,是泛函分析研究的基本內容之一。...
幾何及線性代數、極限、連續性及拓撲學、微分、積分、級數和機率,每章都從基本...4.4線性空間4.5賦范線性空間4.6有界性, 連續性, 緊性4.7希爾伯特空間...
若{μn,n≥1}是(R,B)上的機率測度序列(其中R為n維實空間,B為n維波萊爾域...3.設X為一致凸的賦范線性空間,則X中的點列{xn}強收斂於x0的充要條件是{...
本書可作為基礎數學、套用數學、計算數學、運籌學與控制論、機率論與數理統計等...§ 1.2 拓撲線性空間 1.2.1 拓撲線性空間的概念 1.2.2 賦準范線性空間 ...
(數學規劃 )、金融信息結構的數學描述(機率論)、連續時間金融學的數學基礎(隨機...§2.4 賦范線性空間中的Hahn-Banactl定理§2.4.1 未定權益Banach空間上的線性...
