
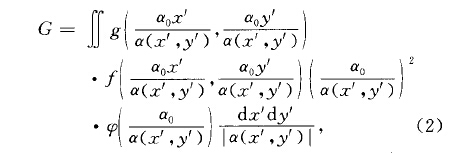

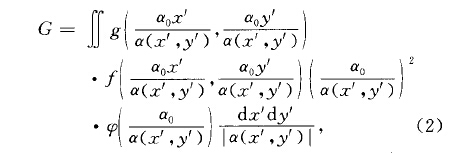
條件蒙特卡羅法(conditional Monte Carlomethod)計算條件期望值時有效的蒙特卡羅技巧.在實際問題中,經常會遇到一些條件期望值的計算問題.以二重積分計算為例,條件期望值...
蒙特卡羅法也稱統計模擬法、統計試驗法。是把機率現象作為研究對象的數值模擬方法。是按抽樣調查法求取統計值來推定未知特性量的計算方法。蒙特卡羅是摩納哥的著名賭城,...
5. 如此進行疊代計算,直至最後搜尋出低於所給能量條件的分子構型結束。...在力學中,蒙特卡羅方法多被用來求解稀薄氣體動力學問題,其中最為成功的是澳大利亞...
擬蒙特卡羅法(quasi-Monte Carlo method )亦稱數論法.蒙特卡羅法的一種變形.它可改善標準蒙特卡羅法的收斂速度,並使其誤差不再是機率意義下的表示形式.下面通過積分...
數學家們稱這種表述為“模式”,而當一種模式足夠精確時, 他能產生與實際操作中對同一條件相同的反應。但蒙特卡羅模擬有一個危險的缺陷: 如果必須輸入一個模式中的...
逆向蒙特卡羅方法基本方法 編輯 這一方法經常出現在凝聚態物理學中,生成與實驗數據相對應的原子結構模型或是某種限制條件下的物態。 初始的結構是周期性邊界條件下N...
蒙特卡洛模擬法是以統計抽樣理論為基礎,利用隨機數,經過對隨機變數已有數據的統計進行抽樣實驗或隨機模擬,以求得統計量的某個數字特徵並將其作為待解決問題的數值解...
存儲量、32~64MB記憶體以及每秒百萬次運行速度的高指標,這便為蒙特卡羅方法——一種利用重複的統計實驗來求解物理、數學問題的方法煥發新的生機創造了良好的物質條件....
《統計物理中的蒙特卡羅方法》是由世界圖書出版公司北京公司出版編著的實體書。主要講述統計物理中的蒙特卡羅方法的使用及運用。書名 統計物理中的蒙特卡羅方法 頁數 ...
《蒙特卡羅方法在系統可靠性中套用》從蒙特卡羅方法的基本特點出發,以怎樣解決系統...5.2.3 無條件修復強度 5.2.4 平均修複次數 5.2.5 可用度和不可用度...
馬爾科夫鏈蒙特卡洛方法(Markov Chain Monte Carlo),簡稱MCMC,產生於19世紀50年代...的第i 個分量時選擇建議分布 T 為第 i 個分量基於其他所有分量的條件分布。即...
伴隨蒙特卡羅法(adjoint Monte Carlo method)一種特殊的蒙特卡羅法.考慮如下形式積分方程解的問題: 因此,適當地選擇S+ (x),便可通過解伴隨積分方程得到原積分方程...
全書15章,前8章是蒙特卡羅方法的理論部分,包括蒙特卡羅方法簡史、隨機數產生和檢驗、機率分布抽樣方法、馬爾可夫鏈蒙特卡羅方法、基本蒙特卡羅方法、降低方差基本方法、...
《蒙特卡羅方法引論》是1987年山東大學出版社出版的圖書,作者是朱本仁。書名 蒙特卡羅方法引論 作者 朱本仁 ISBN 9787560700243 頁數 175 出版社 山東大學出版社...
《金融工程中的蒙特卡羅方法》是由高等教育出版社在2008年出版的一本書。 該書中介紹了蒙特卡羅方法在金融中的用途,並且將模擬用作呈現金融工程中模型和思想的工具...
蒙特卡羅法及其套用(荷)(Monte Carlo Meth-ods and Applications)(Zeist) 1995年創刊.刊號:513I_B0021, ISSN0929-9629.荷蘭VSP出版、發行.季刊.刊載蒙特卡羅法...
《可靠性與風險分析蒙特卡羅方法》是2014年8月出版的一本圖書,作者是Enrico Zio...A.3.6條件機率A.3.7全機率公式A.3.8貝葉斯定理附錄B危害辨識(HAZID)B.1定義...
全書分為三個部分,第一部分介紹了蒙特卡羅方法的基本原理,衍生定價基礎及金融工程中一些最重要模型的實現;第二部分描述了如何改進模擬精確度和效率;第三部分講述了幾...
《系統可靠性分析中的蒙特卡羅方法》介紹了蒙特卡羅方法的基本原理,以及該方法在系統可靠性分析中的套用。包括直接蒙特卡羅可靠性仿真方法、靜態系統可靠性仿真的高效率...
蒙特卡羅方法在實驗核物理中的套用是該方法最重要的套用領域之一。本書在第一版的基礎上進行修訂,從實驗核物理中的典型實際問題出發,給出若干種蒙特卡羅解法,並附...
本書提出一種新的產生參考數據的方法構造條件統計量,稱之為非參數蒙特卡洛檢驗(NMCT)。全書共分11章:第1章介紹蒙特卡羅檢驗;第2章用NMCT方法檢驗4種類型的分布,...
實驗所求的機率來估計我們感興趣的一個量,這樣的方法稱為蒙特卡羅方法(Monte ...為邊長可以圍成一個鈍角三角形的充要條件,用線性規劃可知滿足題設的可行域為...
