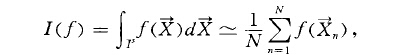



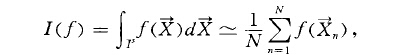



擬蒙特卡羅方法,與蒙特卡羅相似,但理論基礎不同的方法—“擬蒙特卡羅方法”(Quasi-Monte Carlo方法)—近年來也獲得迅速發展。我國數學家華羅庚、王元提出的“華—王...
擬蒙特卡羅法(quasi-Monte Carlo method )亦稱數論法.蒙特卡羅法的一種變形.它可改善標準蒙特卡羅法的收斂速度,並使其誤差不再是機率意義下的表示形式.下面通過積分...
但蒙特卡羅模擬有一個危險的缺陷: 如果必須輸入一個模式中的隨機數並不像構想的那樣是隨機數, 而卻構成一些微妙的非隨機模式, 那么整個的模擬(及其預測結果)都...
蒙特卡羅法也稱統計模擬法、統計試驗法。是把機率現象作為研究對象的數值模擬方法。是按抽樣調查法求取統計值來推定未知特性量的計算方法。蒙特卡羅是摩納哥的著名賭城...
蒙特卡羅方法又稱統計模擬法、隨機抽樣技術,是一種隨機模擬方法,以機率和統計理論方法為基礎的一種計算方法...
蒙特卡洛模擬法是以統計抽樣理論為基礎,利用隨機數,經過對隨機變數已有數據的統計進行抽樣實驗或隨機模擬,以求得統計量的某個數字特徵並將其作為待解決問題的數值解...
蒙特卡洛隨機模擬法的原理是當問題或對象本身具有機率特徵時,可以用計算機模擬的方法產生抽樣結果,根據抽樣計算統計量或者參數的值;隨著模擬次數的增多,可以通過對各次...
蒙特卡羅方法在金融工程學,總量經濟學,生物醫學,計算物理學(如粒子輸運計算、量子熱力學計算、空氣動力學計算、核工程)等領域套用廣泛。...
蒙特卡羅模型是一種隨機模擬方法。以機率和統計理論方法為基礎的一種計算方法。將所求解的問題同一定的機率模型相聯繫,用電子計算機實現統計模擬或抽樣,以獲得問題的...
基於馬爾科夫鏈蒙特卡羅方法的道路圖像分割[D].南京理工大學,2013. 3. 馬傑靈. 不同點列在擬馬爾科夫鏈蒙特卡羅中的套用[D].清華大學,2013....
本書不僅介紹了蒙特卡羅方法在系統可靠性與風險分析中的基本套用,還包括最前沿的研究進展,對可靠性與風險分析的相關研究工作具有重要的參考價值。 [1] ...
最小二乘蒙特卡洛模擬的基本原理:首先,生成標的資產價格的樣本路徑。其次,從期權到期日開始逆向求解,得到每條樣本路徑上的最優期權執行時間和相應的期權收益。最後,將...
《統計物理學中的蒙特卡羅模擬(第5版)(英文版)》主要處理凝聚態物理學的多體系統和相關物理學、化學及其他方面的計算模擬,甚至滲透到交通流、股票市場波動等等領域...
全書共分十一章,分別介紹了隨機模擬方法的特點與步驟、機率論預備知識、Matlab軟體的基本編程方法、隨機數的生成方法、馬爾可夫鏈蒙特卡羅方法、隨機服務系統模型、...
《軟物質的計算機模擬與理論方法》是2010年化學工業出版社出版的圖書,作者是楊...5 雜化蒙特卡羅和廣義系綜模擬方法6 構象態躍遷行為與玻璃化轉變7 表面活性劑與...
正交分解方法等方面闡述了數值計算方法的主要進展,同時較詳細地介紹了介觀與微觀方法(格子-玻爾茲曼方法、直接模擬蒙特卡羅法和分子動力學模擬);在套用篇部分,分別從...
蒙特卡洛擴散模擬又稱隨機遊走擴散模擬,是利用計算機產生大量粒子的隨機遊走軌道模擬湍流擴散。一般作法是想像式地釋放成千上萬個粒子模擬污染物質,各個粒子每次都以一...
隨機模擬也稱蒙特卡羅法或統計試驗法,這種計算方法以機率與統計理論為基礎,由威勒蒙和馮紐曼在20世紀40年代為研製核武器而首先提出,在此之前,作為該方法的基本思想,...
由於反演法有一定局限性,只適用於線性系統,每次模擬只能對固定的時刻求解。後來逐漸被蒙特卡羅法和協方差分析法代替。V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數...
由於要得到這些方程的解析解幾乎是不可能的,所以總是採用數值解法,如:對於常微分方程主要採用各種數值積分法,對於偏微分方程則採用有限差 分法、特徵法、蒙特卡羅法...
對當前解重複“產生新解→計算目標函式差→接受或捨棄”的疊代,並逐步衰減t值,算法終止時的當前解即為所得近似最優解,這是基於蒙特卡羅疊代求解法的一種啟發式...
4)模型的數字方法信用組合觀點方法使用重複的蒙特卡羅模擬法來生成巨觀的衝擊和貸款組合損失或貸款價值的分布,從而最終也能算出風險價值。...
水文隨機模擬(stochastic modeling of hydrologic time series),是用水文時間序列分析的方法,對給定的水文時間序列建立模型,再套用蒙特卡羅方法按選用的模型生成人工序列...
