基本介紹
析因試驗是一種多因素的交叉分組試驗。它不僅可檢驗每個因素各水平間的差異,而且可檢驗各因素間的互動作用。兩個或多個因素間如存在互動作用,表示各因素不是各自獨立的,而是一個因素的水平有改變時,另一個或幾個因素的效應也相應有所改變;反之,如不存在互動作用,表示各因素具有獨立性,一個因素的水平有所改變時不影響其他因素的效應。下面介紹最簡單的兩因素析因試驗(以“2×2”為例)和較複雜的四因素析因試驗(以“2×2×3×2”為例)的設計及其分析方法。
2×2析因試驗
2×2設計表示有兩個因素,每個因素各有兩個水平,共有四個組合。如以A1表示A因素1水平,A2表示A因素2水平,B1表示B因素1水平,B2表示B因素2水平,各因素的水平之間逐個組合,即成2×2設計,其模型如下:
 圖1
圖12×2析因分析時,首先應對4個組合的試驗結果作
方差齊性檢驗,如已滿足齊性要求,即可進行
方差分析。方法如下:
(1)作檢驗假設。有兩種: 一是A因素或B因素的各水平間的比較,H0為A因素或B因素兩水平的總體均數相等,即μ1=μ2;二是分析A、B兩因素的互動作用,H0為兩因素間無互動作用,即彼良槓櫃此獨立。
(2)將總變異的
離均差平方和SS及自由度v按變異來源分為A因素、B因素、互動作用A×B及誤差四部分。SS
A和SS
B的計算公式見條目“單因素多個樣本重漿端均數比較”。A、B兩因素互動作用的離均差平方和SS
A×B的計算需先列副表,再用式(1)及式(2)。
式中SS
T(AB)為A、B兩因素副表總變異的離均差平方和;X
A1B1為A因素1水平與B因素1水平組合的樣本觀察值,余類推;n為分子中每個合計所包含的例數,C'為校正數(C'區別於因素C)。自由度v的計算:總變異v=總例數-1,某因素v=該因素的水平數-1,互動作用v=有關因素的自由度之積,2×2析因分析中v均為1。
(3)分別計算各因素及互動作用料棵妹的均方MS(=SS/v),並與誤差的均方相比得F值。
(4)查F界值表得P值,按所取檢驗水準作出推斷結論。
2×2×3×2析因試驗
2×2×3×2設計,表示有四個因素,各因素依次有2、2、3、2個水平,共有2×2×3×2=24個組合。如以ABCD表示四個因素,A1、A2表示A因素的兩個水平,同樣,B1、B2,C1,、C2、C3,D1、D2分別表示B、C、D因素的各個水平,則2×2×3×2設計的模型如下:
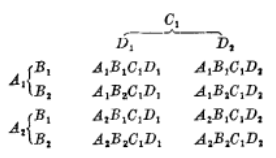 圖2
圖2 圖3
圖3 圖4
圖4按此模型安排24個組合的試驗,每個試驗可根據試驗條件和具體要求規定重複次數,一般所取次數較少。對試驗結果應先作方差齊性檢驗,然後再作方差分析(參照2×2析因分析加以擴展):
單因素組間比較: A,B,C,D;
一級互動作用: A×B,A×C,A×D,B×C,B×D,C×D;
二級互動作用: A×B×C,A×B×D,A×C×D,B×C×D;
三級互動作用: A×B×C×D。
總共15次檢驗,目的在於得出各因素的最佳水平及其組合。
析因試驗能夠分析多種互動作用,以獲得豐富的結論,但當因素過多,因素中包括的水平又劃分過細時,將使互動作用的內容頭緒繁多,不但計辨夜微備算不便,而且對它們的具體解釋亦十分錯綜複雜。故除非必須良頸同時對某些因素進行研究外,一般宜採用較簡單的析因試驗。
析因試驗設計
析因試驗設計是指任意r(r≥1)個因子,每個因子取任意給定數目m
i(i=1,2,店匪悼櫃…,r)水平的試驗的設計,分為全面析因試驗設計和部分實施析因試驗設計兩大類,其中因子的水平是可以控制的或者隨機選取的。每個因子各取一個水平,r個水平構成一個水平組合,總共有n=m
1×…×m
r個不同的水平組合 (亦稱試驗點或處理方法)。對每一水平組合至少進行一次試驗(對一個單元進行試驗)的設計,稱做全面設計,其優點是能考察全部主因子效應和全部互動效應,其缺點是工作最大甚至無法實施,結果也難以控制。1946年芬尼(D.J.Finney)提出了部分實驗法,即只挑選一部分有代表性的水平組合進行試驗的方法,欠芝閥其實質是忽略全部或大部不顯著互動效應(如,忽略全部三階及三階以上互動效應),
正交拉丁方和
正交表就是部分實施的重要工具。
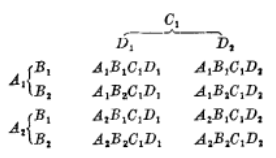 圖2
圖2 圖3
圖3 圖4
圖4按此模型安排24個組合的試驗,每個試驗可根據試驗條件和具體要求規定重複次數,一般所取次數較少。對試驗結果應先作方差齊性檢驗,然後再作方差分析(參照2×2析因分析加以擴展):
單因素組間比較: A,B,C,D;
一級互動作用: A×B,A×C,A×D,B×C,B×D,C×D;
二級互動作用: A×B×C,A×B×D,A×C×D,B×C×D;
三級互動作用: A×B×C×D。
總共15次檢驗,目的在於得出各因素的最佳水平及其組合。
析因試驗能夠分析多種互動作用,以獲得豐富的結論,但當因素過多,因素中包括的水平又劃分過細時,將使互動作用的內容頭緒繁多,不但計算不便,而且對它們的具體解釋亦十分錯綜複雜。故除非必須同時對某些因素進行研究外,一般宜採用較簡單的析因試驗。
析因試驗設計是指任意r(r≥1)個因子,每個因子取任意給定數目m
i(i=1,2,…,r)水平的試驗的設計,分為全面析因試驗設計和部分實施析因試驗設計兩大類,其中因子的水平是可以控制的或者隨機選取的。每個因子各取一個水平,r個水平構成一個水平組合,總共有n=m
1×…×m
r個不同的水平組合 (亦稱試驗點或處理方法)。對每一水平組合至少進行一次試驗(對一個單元進行試驗)的設計,稱做全面設計,其優點是能考察全部主因子效應和全部互動效應,其缺點是工作最大甚至無法實施,結果也難以控制。1946年芬尼(D.J.Finney)提出了部分實驗法,即只挑選一部分有代表性的水平組合進行試驗的方法,其實質是忽略全部或大部不顯著互動效應(如,忽略全部三階及三階以上互動效應),
正交拉丁方和
正交表就是部分實施的重要工具。
 圖1
圖1
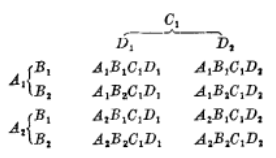 圖2
圖2 圖3
圖3 圖4
圖4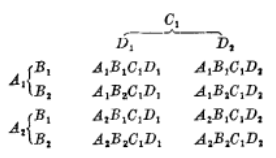 圖2
圖2 圖3
圖3 圖4
圖4
