概念 板筋的使用在建築等領域積累了豐富的設計經驗,同時也提出一些新問題。以水電機組為例,
發電機 上、下機架、轉子支架等許多部件屬於板筋結構。為提高電站綜合效益,當前動力設備的發展趨向於大容量、高負載機組。正在開發的三峽水力機組,單機最大容量達到70 萬kW,下機架負載5500t。容量的增大帶來剛度、強度、穩定性、絕緣等方面一系列問題。結構方面,為保障安全,採取的辦法往往是按比例增加板筋件尺寸,結果造成板筋件尺寸越做越大,占用的空間隨之增加。
問題的探討 “強柱弱梁”作為我國抗震規範抗震措施中重要的一條,對於 9 度區及一級抗震等級,它要求節點處柱上、下端實際受彎
承載力 之和在地震作用效應下應大於梁端受彎承載力之和。但當考慮現澆樓板內板筋對框架梁抗彎能力的提高作用時,究竟需對柱端彎矩設計值增大多少,才能滿足“強柱弱梁”的要求,一直是設計界懸而未決的問題。而其中怎樣考慮板筋作用以及考慮多少範圍內的板筋則是這個問題的關鍵。
中國規範現狀
我國新頒布實施的《混凝土結構設計規範》(GB 50010 -2002)和《建築抗震設計規範》(GB 50011-2001) 提高了“強柱弱梁”的彎矩增大係數,規定 9 度及一級框架結構尚應考慮框架梁的實際受彎
承載力 ;並在《建築抗震設計規範》條文說明中指出“彎矩增大係數考慮了一定的超配鋼筋和鋼筋超強”,但對框架梁翼緣現澆板內與梁肋平行的鋼筋參與梁端負彎矩承載能力的問題,新規範仍未作明確的規定,只是在《建築抗震設計規範》條文說明中附帶指出,當計算梁端抗震承載力時,若計入樓板內的
鋼筋 ,且材料強度標準值考慮一定的超強係數,則可以提高框架結構“強柱弱梁”的程度。對比實驗表明,由於梁翼緣現澆板內平行於梁肋的鋼筋參與形成梁端抗彎承載力,
在所試驗的梁—柱組合體試件中,支座處的負屈服彎矩要比無翼緣矩形梁的負屈服彎矩提高 30%左右。如果把數值1.3作為板筋參與係數考慮到“強柱弱梁” 彎矩增大係數中去,就可以發現新規範的仍然是遠遠不夠的。當然,由於板內平行於框架的板筋相對數量差異較大,板筋對梁端負彎矩承載力的增大係數並非總是1.3,但唐山地震中整體現澆梁板框架的破壞大多發生在柱上,而沒有現澆樓板的空框架裂縫則都顯示在框架樑上的事實從一個側面證明了這一點。
國外規範對板筋參與梁端負彎矩受力的規定
鑒於中國規範對這方面的有關問題仍未明確,因此,了解國外有關規範對此作出的規定,對我國設計界正確處理有關問題是有益的。
在考慮板筋參與問題上各國思路之間也有原則性差別。其中紐西蘭規範明確規定,在進行梁端截面抗負彎矩設計時,即確定設計所需的負彎矩鋼筋時,可以考慮板有效寬度範圍內的與梁肋平行的上板面和下板面板筋作為負彎矩受拉鋼筋的組成部分。因此,按該規範算出的梁負彎矩筋就只是除去相應板筋外所需要的受拉鋼筋。當按實配確定梁端抗彎能力時,自然就必須把已考慮的板筋計入,而且在沒有人為增大配筋量的前提下,考慮板筋後的梁端抗負彎矩能力與作用負彎矩應沒有大的差別。所以,按紐西蘭的上述思路,板筋不屬於“超配”,自然在“強柱弱梁”的措施中也就可以不考慮板筋引起的“超配”問題。
而美國 ACI 規範,加拿大 CSA 規範以及
歐共體 EC8 規範在作梁端抗負彎矩截面設計時與中國思路一樣,未要求考慮板筋,但與中國規範不同的是,中國規範是將設計所需的梁端負彎矩筋與無現澆板的框架梁一樣布置在梁肋頂部的寬度範圍內,而這三本規範規定梁端計算出的負彎矩筋除了大部分應放在肋寬範圍內,少部分則可放在規範規定的一定板寬範圍內。其中美國和加拿大規範認為這樣做的目的是避免上部板筋過於擁擠和避免在臨近梁肋的板內出現過寬的裂縫。因此,當按實配確定梁端抗彎能力並考慮有效寬度內與梁筋平行的鋼筋時,這部分鋼筋可能既有原設計所需的受拉鋼筋,又有額外的板筋,而只有額外的板筋才屬於“超配”部分。
國內外研究成果分析
Pantazopoulou 等人曾建議了一種確定板的
有效寬度 的理論方法,該方法首先假設了在板截面中的非線性應變分布函式,然後根據鋼筋性能、梁中最大應變和板的最大寬度導出一個有效板寬的表達式,並給出了適用於中間節點和端節點的不同模型。但美國的一些學者如 French 等人對Pantazopoulou 的模型分析後認為,板對梁抗彎能力的貢獻取決於一系列變數,其中包括節點的類型(中間節點還是端節點)、直交梁剛度,側向變形的水準以及水平載入的特徵(單軸還是雙軸),當前看來還沒有找到能適當考慮所有有關變數的解析解。
美國 M . R . Ehsani 等人於1982年曾做了 6 個帶直交梁和
樓板 (板厚 4 英寸)的足尺邊節點試驗,設計時考慮梁的每側只有二根樓板縱向鋼筋參與梁的抗彎作用,但是實測表明,40 英寸寬的樓板內所有板筋都達到屈服,導致梁的抗彎強度增大,結果造成塑性鉸在板面以上的柱端形成。因此他們建議在實際結構中對於帶樓板和直交梁的節點,在計算梁的
抗彎強度 時,應考慮主梁每側至少各一倍梁寬範圍內的樓板縱向鋼筋作用,即有效寬度為 3 倍梁寬。
1987 年同濟大學和中國建築科學研究院與日本、紐西蘭和美國進行合作,作了 6 個足尺的雙向節點試驗,其中有兩個是帶樓板(板厚100 mm,配有雙層雙向鋼筋φ10 @175 mm) 的雙軸受力節點。試驗表明,樓板明顯提高了梁負彎矩抗彎能力,樓板的有效寬度隨位移延性加大而增大,當μΔ =1 時,影響寬度達 740 mm,當 μΔ =3 時達1732 mm。
1994 年東南大學蔣永生等人進行了一個梁板整澆的和一個沒有板的框架中節點的對比實驗。試驗表明,梁板整澆的框架節點,在梁頂面受拉鋼筋屈服的同時,靠近梁的部分板內上部
鋼筋 亦達到屈服;當 μ
Δ =3 時達最大承載力,此時梁側 6 倍板厚範圍內板頂、底面的鋼筋均達到屈服。根據試驗結果他們認為對於梁板現澆的框架節點,當梁端上部受拉時,應考慮平行於框架梁且有足夠錨固長度的板內鋼筋參與工作,並認為可近似取梁每側六倍板厚範圍作為板的有效寬度。
美國學者 French 等人收集和總結了各國 20 個梁-板-柱節點(13 箇中節點、7 個端節點)試驗結果,對獲得的數據進行分析後認為,如果將板的有效寬度取為 ACI 規範規定的有效寬度,則計算出的
抗彎強度 就將接近於實測的當層間水平位移角為2%( 約相當於位移延性係數為4) 時的抗彎強度;同時 French 也指出,由於板的作用是極其複雜的,它與許多變數有關,而所獲得的實驗數據依然非常有限,因此對板有效寬度的確定仍然帶有很大的近似性。
圖 1 典型板筋應變圖 應該指出的是,板有效寬度是一種折算寬度,不是板的實際參與寬度,也不是板參與梁抗彎時所能達到的屈服寬度。圖 1 給出了一個典型的實測板筋的應變分布圖,從圖中可以看出,無論是上部板筋還是下部板筋,都有較大寬度範圍內的板筋參與工作,但只有很小寬度範圍的板筋達到屈服。板有效寬度實際上是將板所提供的有效抗彎能力折算成一定範圍內板完全參與受彎(即考慮達到屈服)的一種折算寬度。
研究結論
(1)板
有效寬度 是一種計算折合寬度,不是板的實際參與寬度,也不是板參與梁抗彎時所能達到的屈服寬度。
(2)根據按中國規範設計的典型框架所能達到的最大層間位移角,可取梁每側六倍板厚範圍作為板的有效寬度。
(3)對框架端節點來說,當直交邊梁的抗彎和抗扭剛度與縱梁相比不至於相差太多時,在端節點處仍然可以取梁每側六倍板厚作為板的有效寬度;但如果直交邊梁剛度偏弱,則板的有效寬度取值應相應減少。
(4)在考慮板筋參與梁端抗彎的同時,應注意參與受力板筋的錨固問題和板內與梁垂直方向橫向鋼筋的設定問題,以保證縱向板筋能有效的參與梁端抗彎。
最佳化方法 研究背景
有效的板筋最佳化不僅可以合理地組織結構、充分利用空間、挖掘材料潛能,而且可以降低產品成本,減少單機容量增大引發的負面效應。此外,對比相同容量、同期開發的國內外水電機組可以發現,國內獨立設計的機組較厚重,國外設計的機組(如日立/馬卡古瓦,CE/清江)相對較輕薄。產生這種局面的原因在於國外對機組方案,除必要的校核、分析外,最佳化是必不可少的環節。
繼桁架最佳化方面取得的成果之後,國內一些單位陸續開展了板、實體最佳化方面的研究。程耿東對薄板結構進行了分析,易澤明、李彩雲等套用規劃法分別對離心機、
懸臂結構 進行了實體最佳化,方剛、康達昌對薄壁箱形體進行了準則最佳化,楊學貴等對薄壁殼體進行了最佳化,陳新、何杰等對板、實體混合結構(工具機床身)進行了最佳化分
析。
板筋結構是板、筋的有效組合,但板筋最佳化不是板、梁最佳化的簡單疊加。由於連線方式不同,板筋結構分為兩大類。最佳化時,需要對其類型進行判別,並進行有針對性建模;同類型的板筋結構中,不同位置的承載板,分為拉壓板、彎板及混合板三種情況,需要選用不同的中間變數;梁、板、實體三種單元共存的模型中,應使自由度、最佳化變數滿足協調條件。板筋最佳化牽扯到尺寸、形狀、拓撲三方面內容,根據實際情況,可以選擇準則法、規劃法或混合法。對於大型板筋結構,針對有限元模型進行最佳化時,需要保證算法的穩定性。
最佳化分析的執行步驟
最佳化的方法很多,對於無約束問題,可以採用牛頓法、單純形法、最速下降、共拓梯度法:對於有約束問題,可以採用復形法、可行方向法、梯度法等方法,也可以通過變換將有約束最佳化問題化為無約束問題解決。對大型結構問題,包括板筋結構,研究建議採用中間變數以及近似( 二次/一次) 手段,將非線性的目標/約束函式,用一次/二次函式逼近。然後利用
拉格朗日 乘子( 或
罰函式 ) 將有約束問題化為無約束問題。尺寸最佳化時,選擇擬牛頓法求解;形狀最佳化中,可以採用對偶規劃,減少約束數目,並利用線性規劃法求解。
研究立足於
有限元 模型組織最佳化過程。首先建立板筋結構的有限元模型,判別其類型,並劃分單元、節點群組,選擇適當的最佳化變數和約束條件;其次根據最佳化類型進行相關的算法解算;經疊代取得有效結果後,將數值代回原始結構,進行方案更改。
研究結論
繼桁架最佳化方面的成果之後,隨著有限分析能力的提高,國內許多行業開始探索板筋結構最佳化方法,對此作了總結。對板筋結構最佳化定義,目標/約束條件處理及具體求解進行了闡述。圍繞規劃法,研究對一些相關概念進行了說明。最後,以小浪底下機架實例,證明了所述方法的可行性。對兩類板筋結構,研究比較了兩者在結構和功能上的區別,提出建模、最佳化方面的建議。事實證明,對筋和筋板連線的不同處理,直接影響最佳化結果,以及結構方案的改進。
對大型板筋結構,由於涉及到的單元類型多,受力狀況複雜,最佳化時,建議採用比較成熟的線性(或二次近次) 算法,以利於計算收斂。
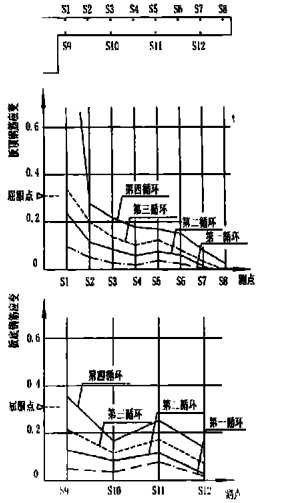 圖 1 典型板筋應變圖
圖 1 典型板筋應變圖
