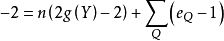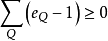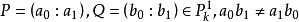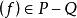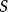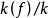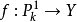基本介紹
- 中文名:有理曲線
- 外文名:rational curve
- 定義:虧格式0的代數曲線就是有理曲線
- 性質1:有理曲線的虧格是0
- 性質2:有理曲線和射影直線同構
- 套用學科:代數曲線
簡介,定義,表述一,表述二,相關定理,定理一,定理二,定理三,定理四(Luroth定理),
簡介
有理曲線是為了統一表示自由曲線和圓錐曲線而發展起來的,它與普通Bezier曲線,B-Spline曲線一樣,是一種逼近形式,有很好的幾何直觀性,通過對控制頂點的調整,即可實現對曲線形狀的控制,同時有理曲線上每個頂點上的權因子又為形狀控制提供了新的自由度。綜合使用以權因子為基礎的方法和以控制頂點為基礎的方法可以對曲線形狀進行更為直觀、快速準確的控制,在飛機、輪船、汽車等複雜外形產品的幾何設計中有實用價值。
定義
表述一
表述二
虧格式0的代數曲線就是有理曲線。
相關定理
定理一
射影直線 是有理曲線。
是有理曲線。

證明: 的函式域
的函式域 ,則
,則 。
。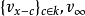 是
是 的全部標準離散賦值。設其對應的賦值環為
的全部標準離散賦值。設其對應的賦值環為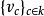 和
和 ,則
,則 是
是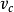 的極大理想的生成元,
的極大理想的生成元, 是
是 的極大理想的生成元。因
的極大理想的生成元。因 對所有的
對所有的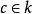 成立,因此
成立,因此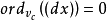 對所有的
對所有的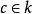 成立。又因
成立。又因 ,得
,得 ,故有
,故有 ,因此
,因此 的虧格為零。
的虧格為零。



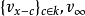

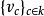


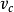



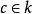
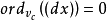
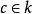




定理二
設X 是光滑的射影曲線,則X同構於 ,若且唯若存在X上兩個不同點P,Q相互線性等價。
,若且唯若存在X上兩個不同點P,Q相互線性等價。

定理三
有理曲線同構於射影直線 。
。

定理四(Luroth定理)
證明:設n是 的次數,則根據Hurwitz公式有
的次數,則根據Hurwitz公式有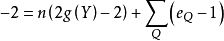 ,因
,因 ,
,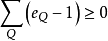 ,故
,故 。
。