有向球面三角形(directed spherical triangle)亦稱定向球面三角形,是球面三角形的一種,指規定了三個頂點順序的球面三角形。
基本介紹
- 中文名:有向球面三角形
- 外文名:directed spherical triangle
- 所屬學科:數學
- 所屬問題:幾何學(球面幾何)
- 相關概念:球面三角形,球面角等
基本介紹
相關概念
球面三角形





有向球面角
有向角
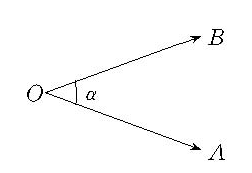
球面角
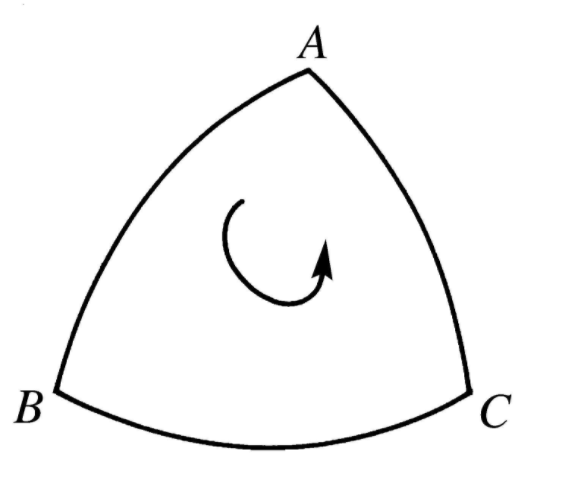
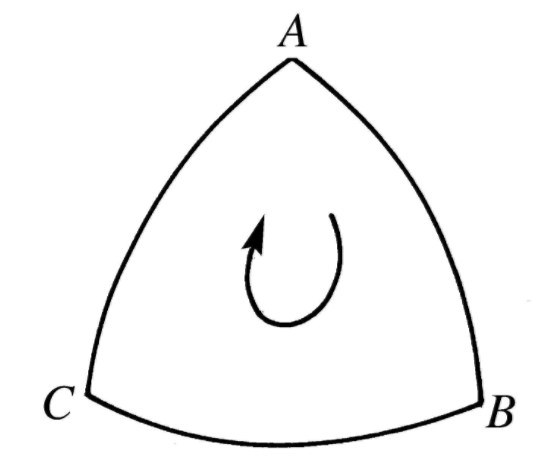
有向球面三角形(directed spherical triangle)亦稱定向球面三角形,是球面三角形的一種,指規定了三個頂點順序的球面三角形。










有向球面三角形(directed spherical triangle)亦稱定向球面三角形,是球面三角形的一種,指規定了三個頂點順序的球面三角形。基本介紹有向球面三角形亦稱定向球面三角形,是球面三角形的一種,指規定了三個...
球面三角是研究球面三角形的邊、角關係的一門學科。從十六世紀起由於天文學、航海學、測量學等方面的發展,球面三角逐漸形成了獨立學科。從平面三角學我們知道,一圓周的1/360 ,叫做1度的弧。1度弧的1/60 叫做1角分的弧。1角分弧的1/60 叫做1角秒的弧。根據弧和所對圓心角的關係,可以得出角的量度。一...
球面三角學是球面幾何學的一部分,主要在處理、發現和解釋多邊形 (特別是三角形) 在球面上的角與邊的聯繫和關聯。在天文學上的重要性是用於計算天體軌道和地球表面與太空航行時的天文導航。球面上的線 在球殼的表面,最短的距離是大圓上接近直線的弧線,也就是圓弧的圓心與球殼的球心是同一點。例如:地球上的...
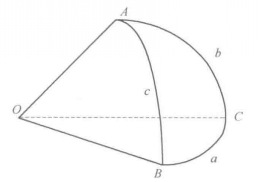
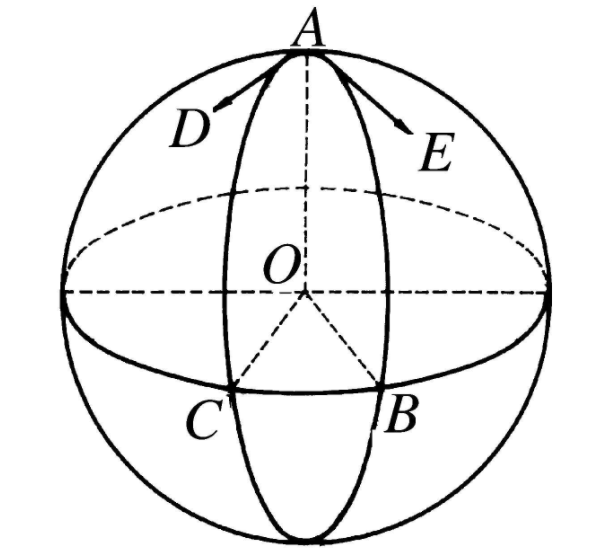
叫做球面三角形的邊,有公共頂點的兩邊組成的角,叫做球面三角形的角,它的大小等於過頂點而切於兩弧的切線夾角。與球面三角形相對應的有一個三面角。如圖2,從球心O經球面三角形的三頂點A、B、C引射線,得到一個以球心為頂點的三面角O-ABC,這個三面角叫做球心三面角,三面角的三個面角對應於球面三角形的...
球面半邊公式(formulas of the spherical half side)是球面三角的基本公式之一,即用與球面三角形各角有關的三角函式表示其各邊之半的三角函式的公式。正弦公式 表達式 證明 設球面三角形 ,如圖1,作球心三角形 ,從球面三角形的任意一個頂點A向平面 作垂線 ,通過垂足 ,在平面 內作 顯然, 連線 ...
直角球面三角形是球面三角形的一種,即只有一個內角是直角的球面三角形,其直角的對邊稱為斜邊,其餘兩邊稱為直角邊或垂邊。在球面三角形的三個角中,可以有一個、兩個或三個直角,含有三個直角的球面三角形稱為三直角球面三角形,它的各邊皆為一象限(如圖1中的球面三角形 ),故又稱象限球面三角形;含有兩個...
由不在同一直線上的三條線段首尾順次連線所組成的封閉圖形叫作三角形。平面上三條直線或球面上三條弧線所圍成的圖形,三條直線所圍成的圖形叫平面三角形;三條弧線所圍成的圖形叫球面三角形,也叫三邊形。由三條線段首尾順次相連,得到的封閉幾何圖形叫作三角形。三角形是幾何圖案的基本圖形。分類 按角分 判定...
三角學是指以研究平面三角形和球面三角形的邊和角的關係為基礎,達到測量上的套用為目的一門學科。同時,三角學還研究三角函式的性質以及它們的套用。內容簡介 三角學(trigonometry)數學的一門分科,包括平面三角學和球面三角學。平面三角學研究三角函式的性質和圖象、三角函式式的恆等變換、解三角形等。球面三角學研究...
全等球面三角形(congruent spherical triangles)是指兩個球面三角形的一種等價關係,即在同球面或等球面上,一個球面三角形的三邊、三角分別與另一個球面三角形的三邊、三角對應相等的兩個球面三角形。基本概念 全等球面三角形:(1)在同一球或等球面上,若兩球面三角形的邊及角分別對應相等,且排列順序一致時,...
斜角球面三角形(oblique angled spherical triangle)是球面三角形的一種,指三個內角都不是直角的球面三角形。三個內角都是銳角的斜角球面三角形,稱為銳角球面三角形;至少有一個內角是鈍角的斜角球面三角形,稱為鈍角球面三角形。基本介紹 定義 斜角球面三角形指三個內角都不是直角的球面三角形。三個內角都是銳角...
這樣,這個大三角形的三個內角和就不是180度,而是90度×3=270度。也就是說客觀上存在著內角和大於180度的三角形。球面幾何學是非歐幾何學的一種。球面的高斯曲率是正數,球面三角形的內角和大於180度(如△DCE)。向內凹陷的曲面,一般叫偽球面,它的高斯曲率是負數,三角形的內角和就是小於180度(如△CAB...
球面極線三角形 球面三角形的三個頂點的極線所構成的三角形,稱為球面三角形的球面極線三角形。
對心球面三角形 對心球面三角形(oppositely central sphericaltriangle)亦稱對頂球面三角形.兩個位置相關的球面三角形。指三個頂點分別互為對徑點的兩個球面三角形.對心球面三角形關於球心成中心對稱.
球面三角形 球面三角是研究球面三角形的邊、角關係的一門學科。從十六世紀起由於天文學、航海學、測量學等方面的發展,球面三角逐漸形成了獨立學科。從平面三角學我們知道,一圓周的1/360 ,叫做1度的弧。1度弧的1/60 叫做1角分的弧。1角分弧的1/60 叫做1角秒的弧。根據弧和所對圓心角的關係,可以得出角的...
球面三角形 球面三角是研究球面三角形的邊、角關係的一門學科。從十六世紀起由於天文學、航海學、測量學等方面的發展,球面三角逐漸形成了獨立學科。從平面三角學我們知道,一圓周的1/360 ,叫做1度的弧。1度弧的1/60 叫做1角分的弧。1角分弧的1/60 叫做1角秒的弧。根據弧和所對圓心角的關係,可以得出角的...
《幾何》是法國數學家M.貝爾熱為大學生撰寫的一套教學參考書.全書共分五卷.主要內容為:群在集合上的作用,仿射與射影空間;歐氏仿射空間;凸集與緊多面體;二次型,二次超曲面與圓錐曲線;球面與橢圓、雙曲幾何.本書配有大量的圖和例,並有許多知識性的注釋、按語和歷史文獻介紹.本卷介紹歐氏空間,三角形,...
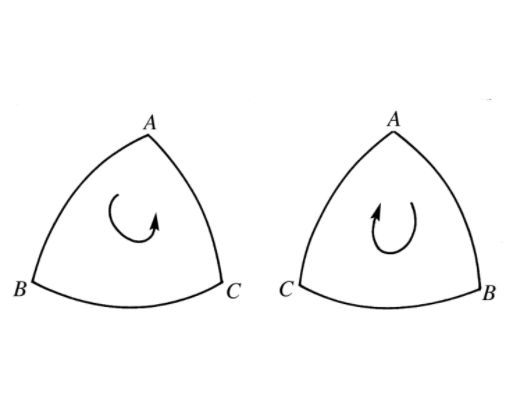
全等球面圖形,兩球面圖形的一種等價關係.若圖形F和F'在同一球面或等球面上,且它們的點之間可建立一一對應關係,使得以F的任意兩點為端點的大圓弧(劣弧)等於以F'的相應兩點為端點的大圓弧,則稱F和F'為全等的球面圖形.全等球面圖形有本質相等和鏡像相等兩種.在兩個全等的球面圖形中,若對應的球面三角形同向(...
將三面角O-ABC的頂點與單位球的球心重合,並設三邊與球面分別交於A、B、C。根據球面三角形的定義,在球面△ABC中,∠AOB=c,∠BOC=a,∠AOC=b;∠OA=A,∠OB=B,∠OC=C。則餘弦定理的第一形式可化為:餘弦定理的第二形式可化為:由於球面三角形與其極對稱三角形之間存在定量的邊角關係,因此不妨設球面...
5.矩形具有平行四邊形的所有性質 三角形 定義 由不在同一直線上的三條線段首尾順次連線所組成的封閉圖形叫做三角形。 平面上三條直線或球面上三條弧線所圍成的圖形。 三條直線所圍成的圖形叫平面三角形;三條弧線所圍成的圖形叫球面三角形,也叫三邊形。內角 內角和為180° 直角 勾股定理,只適用於直角三角形...
地球是一個橢球體,由於橢球扁率的影響,橢球面上的大地問題解算十分複雜。在實際套用中,往往把地球近似看作是一個正球體,這樣,利用球面三角形的相關公式,大圓航線的解算就可以大大地被簡化。在球面上由三個大圓弧相交於三點所圍成的球面部分稱為球面三角形,構成三角形的大圓弧稱為球面三角形的邊,由兩個大...
第四章 球面幾何和球面三角 4.1 球面幾何 4.1.1 球、球面 4.1.2 大圓 4.1.3 球面距離 4.1.4 軸、極、極距、極線 4.1.5 球面角及其度量 4.1.6 小圓弧長與大圓弧長之比 4.1.7 地球上的基本知識 4.2 球面三角 4.2.1 球面三角形的定義 4.2.2 球面三角形的分類 4.2.3 兩個球面三角形...
採用地球面上兩地間最短航線,即大圓航線的球面航法。已知起訖兩點的經緯度,可用球面三角的邊餘弦公式解算由地極和起訖兩點形成的三角形求得航程,再用正弦公式計算起訖點的航向。也可利用大圓頂點將該球面三角形分為兩個直角三角形以簡化計算。這些解法和天文三角形的解法相似,可借用天文航海用表計算。大圓航法發表...
