航法,是指航跡計算和航行方法的合稱。前者用數學計算或査表的方法來確定航向、航程或推算船位,有平面航法、流中航法、折航法、中分緯度航法、墨卡托航法、大圓航法、等緯圈航法、混合航法等八大航法;後者研究船舶在各種不同航海條件下保持在計畫航線上的航行方法,可分為大洋航法、沿岸航法、過水閘航法、運河航法、狹水道航法、霧中航法、冰區航法、島礁區航法等。
基本介紹
- 中文名:航法
- 外文名:sailings
- 方法:用數學計算或查表
- 性質:航行作業方法
簡介,平面航法,流中航法,折航法,等緯航法,中分緯度航法,墨卡托航法,大圓航法,混合航法,常用情況,
簡介
航法(sailings)
15~17世紀,航海家們經過長期實踐和研究總結出八大航法,形成以平面三角和球面三角的解算為基礎的航海學。這八大航法為平面航法、流中航法、折航法、等緯航法、中分緯度航法、墨卡托航法、大圓航法和混合航法。
平面航法
把地球面看作平面的航法。航向、航程、緯差、東西距之間的數學關係可用直角平面三角形表示。圖中,緯差=航程×cos(航向);東西距=航程×sin(航向)。此法計算簡單,曾使用了數世紀。但除用於近距離航行外,準確性差。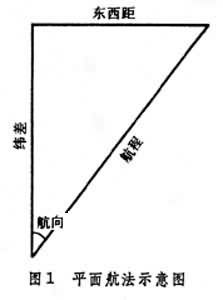

流中航法
把流向、流程當作一個附加的航向、航程的航法。用於流中推算船位或計算能抵消流的影響的駕駛航向。
折航法
多航向的航法。計算時先分別求出各航向段的緯差和東西距的總和,再求直航向和直航程,即相當的單一航向和航程。1436年出現折航表,簡化了計算過程。過去帆船搶風曲折航行常使用此航法,現在機動艦船也使用此法。
等緯航法
東西向航行時,涉及東西距和經差換算的航法。這是最簡單的球面航法,其關係式為:
經差=東西距×sec(緯度)
過去在海上不能測定經度的時代常用此法。現在混合航法中也仍使用。
中分緯度航法
斜向航行時用中分緯度解決經差和東西距換算問題的球面航法(緯差計算同平面航法)。其關係式為:
經差=東西距×sec(中分緯度)
當兩地(緯度同名)的經度線在某緯度圈上所截弧長等於該兩地的東西距時,此緯度稱為中分緯度,在該兩地平均緯度附近。航程200海里以內,可用平均緯度作為中分緯度。航程小於600海里,而且緯度小於60°時,用平均緯度代替中分緯度計算經差所產生的誤差約為 1%。如果要求得到準確值,則要按航海表中的中分緯度修正量表加以修正。中分緯度航法出現於17世紀,用以解決平面航法不準確的問題,雖不如墨卡托航法準確,但仍有用。
墨卡托航法
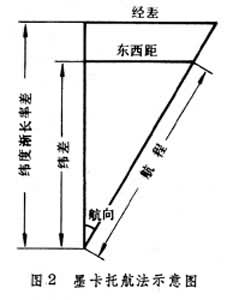
利用墨卡托投影中經度線上的緯度漸長率差進行航行計算的航法,又稱恆向線航法。其關係式為:
經差=緯度漸長率差×tg(航向)
墨卡托投影是在將球面投影於平面時,使經度線和緯度線同比例地漸長。緯度漸長率差就是兩地緯度漸長率之差(緯度同名時相加)。緯度漸長率表發表於1599年,可在航海表中找到,它是墨卡托航法的基礎。此航法很準確,但當靠近東西向航行時應使用中分緯度航法,因正切在90°附近變化很快,航向稍有誤差將引起很大的經差誤差。
大圓航法
採用地球面上兩地間最短航線,即大圓航線的球面航法。已知起訖兩點的經緯度,可用球面三角的邊餘弦公式解算由地極和起訖兩點形成的三角形求得航程,再用正弦公式計算起訖點的航向。也可利用大圓頂點將該球面三角形分為兩個直角三角形以簡化計算。這些解法和天文三角形的解法相似,可借用天文航海用表計算。大圓航法發表於1537年,由於當時對風、流的知識和測定經度的方法尚未掌握,直到19世紀才獲得推廣。
混合航法
當大圓航線受陸地、冰山或惡劣天氣的限制,將大圓航法和其他航法混合使用的航法。此法是將限制緯度作為大圓頂點計算大圓航線,其餘按有關航法計算。
常用情況
航法計算不如海圖作業直觀、簡單,所以一般僅在如下情況使用:①海圖比例尺太小,圖上作業的準確度不夠高時;②在無線電定位和天文定位中,不能直接在海圖上作圖時;③轉向頻繁,難以進行海圖作業時。

