基本介紹
- 中文名:方程回歸
- 外文名:Equation regression
- 描述:回歸分析
- 套用:回歸直線方程
- 學科:數學
名詞解釋
具體計算
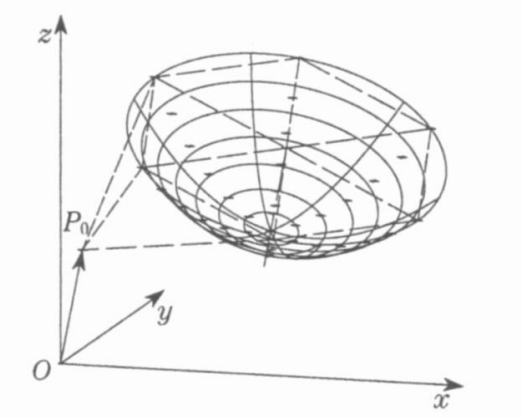
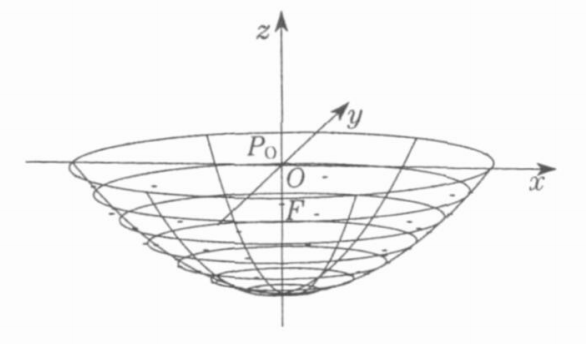
優選方法
理論分析
方法的驗證
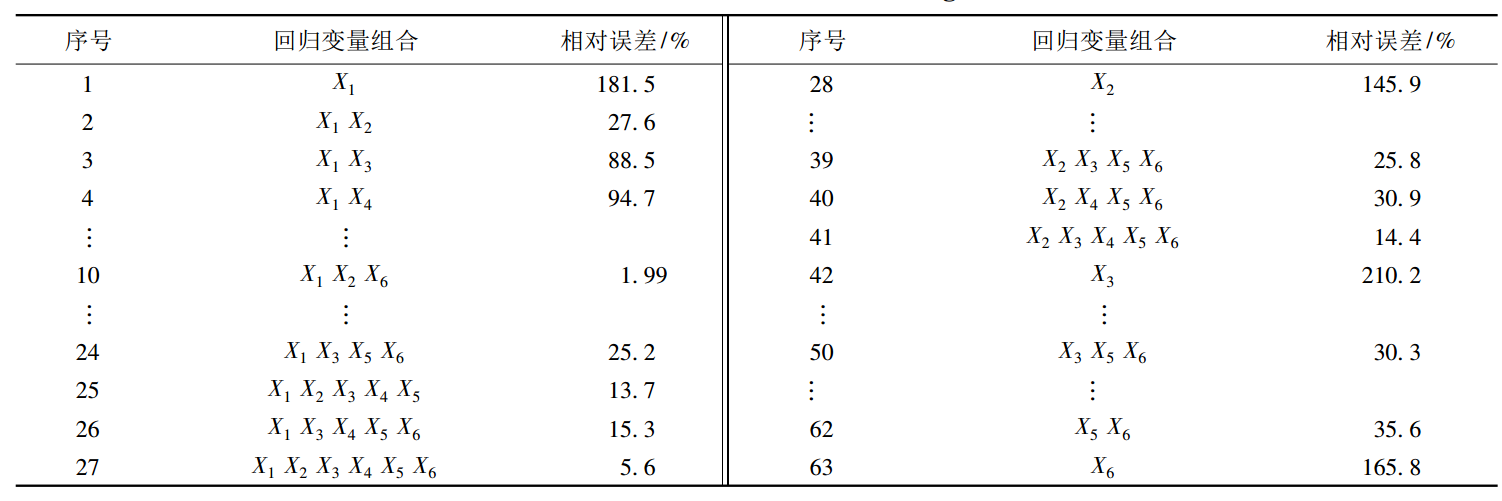
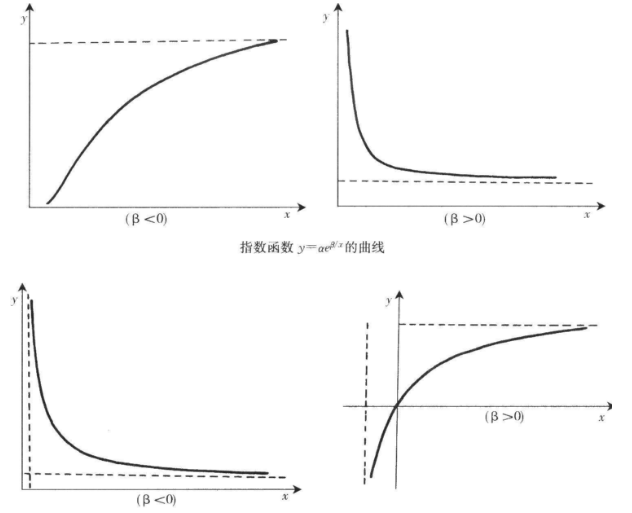



方程回歸是指根據樣本資料通過回歸分析所得到的反映一個變數(因變數)對另一個或一組變數(自變數)的回歸關係的數學表達式。回歸直線方程用得比較多,可以用最小二乘法求回歸直線方程中的a、b,從而得到回歸直線方程。名詞解釋方程回...
回歸方程(regression equation)是對變數之間統計關係進行定量描述的一種數學表達式。指具有相關的隨機變數和固定變數之間關係的方程。回歸直線方程指在一組具有相關關係的變數的數據(x與y)間,一條最好地反映x與y之間的關係直線。運算...
回歸分析就是要找出一個數學模型Y=f(X),使得從X估計Y可以用一個函式式去計算。當Y=f(X)的形式是一個直線方程時,稱為一元線性回歸。這個方程一般可表示為Y=A+BX。根據最小平方法或其他方法,可以從樣本數據確定常數項A與回歸...
在統計學中,線性回歸方程是利用最小二乘函式對一個或多個自變數和因變數之間關係進行建模的一種回歸分析。這種函式是一個或多個稱為回歸係數的模型參數的線性組合。只有一個自變數的情況稱為簡單回歸,大於一個自變數情況的叫做多元回歸...
在SPSS軟體里可以很容易地實現線性回歸,回歸方程如下:y=0.857+0.836x回歸直線在y軸上的截距為0.857、斜率0.836,即質量每提高一分,用戶滿意度平均上升0.836分;或者說質量每提高1分對用戶滿意度的貢獻是0.836分。上面所示的...
回歸直線方程指在一組具有相關關係的變數的數據(x與Y)間,一條最好地反映x與y之間的關係直線。離差作為表示Xi對應的回歸直線縱坐標y與觀察值Yi的差,其幾何意義可用點與其在回歸直線豎直方向上的投影間的距離來描述。數學表達:Yi-y...
邏輯回歸是用來計算“事件=Success”和“事件=Failure”的機率。當因變數的類型屬於二元(1 / 0,真/假,是/否)變數時,我們就應該使用邏輯回歸。這裡,Y的值從0到1,它可以用下方程表示。上述式子中,p表述具有某個特徵的機率。3...
多元性回歸模型的參數估計,同一元線性回歸方程一樣,也是在要求誤差平方和(Σe)為最小的前提下,用最小二乘法求解參數。以二線性回歸模型為例,求解回歸參數的標準方程組為 解此方程可求得b0,b1,b2的數值。亦可用下列矩陣法求得 ...
線性回歸擬合方程 最小二乘法 一般來說,線性回歸都可以通過最小二乘法求出其方程,可以計算出對於y=bx+a的直線,其經驗擬合方程如下:其相關係數(即通常說的擬合的好壞)可以用以下公式來計算:理解回歸分析的結果 雖然不同的統計...
在回歸分析中,用來描述具有線性關係的因變數y與自變數xi的關係曲線,其一般表達式是y=a+∑bixi,i=1,2,…,n。定義 回歸直線方程是根據樣本資料通過回歸分析所得到的反映一個變數(因變數)對另一個或一組變數(自變數)的回歸關係...
如果自變數只有一個時,稱為一元多項式回歸;如果自變數有多個時,稱為多元多項式回歸。在一元回歸分析中,如果變數y與自變數x的關係為非線性的,但是又找不到適當的函式曲線來擬合,則可以採用一元多項式回歸。一元m次多項式回歸方程為:。...
回歸直線方程 在自然界和人類社會的各種現象中 ,同一過程中的變數之間往往存在著一定的關係 .這種關係通常可以分為兩類 ,一類是在微積分中已經詳細研究過的函式關係 ,稱為確定性關係 ;另一類是相關關係 ,稱為非確定性關係 .研究...
正交多項式回歸是用正交多項式表安排試驗和回歸分析處理數據。它與用最小二乘法配製的一般多項式回歸不同,其回歸係數的估計是互相獨立的,若統計檢驗某一回歸係數與零無顯著性差異,只需從回歸方程中刪去這一項,而無需對其他的回歸係數...
在統計學中,線性回歸是利用稱為線性回歸方程的最小二乘函式對一個或多個自變數和因變數之間關係進行建模的一種回歸分析。這種函式是一個或多個稱為回歸係數的模型參數的線性組合。一個帶有一個自變數的線性回歸方程代表一條直線。我們...
前面學到的標準分就有這個功能,具體到這裡來說,就是將所有變數包括因變數都先轉化為標準分,再進行線性回歸,此時得到的回歸係數就能反映對應自變數的重要程度。這時的回歸方程稱為標準回歸方程,回歸係數稱為標準回歸係數,表示如下:由...
回歸方程的精度,對於某一給定自變數值,因變數值的波動程度。這種波動是由於除了被研究自變數之外的其他的因素、隨機誤差以及回歸參數波動的影響造成的。可用回歸方程的標準差來量度 這種波動是由於除了被研究自變數之外的其他的因素、隨機誤差...
為了求出多元線性回歸模型中的參數 ,可採用最小二乘法,即在其數學模型所屬的函式類中找一個近似的函式,使得這個近似函式在已知的對應數據上儘可能和真實函式接近。設 分別是 的最小二乘估計,則多元回歸方程(即近似函式)為:...
所謂回歸分析法,是在掌握大量觀察數據的基礎上,利用數理統計方法建立因變數與自變數之間的回歸關係函式表達式(稱回歸方程式)。與函式關係的區別 直線回歸分析要建立的直線回歸方程表達式是Y=a+bX,這裡的X稱為自變數,Y稱為因變數。X與Y...
多重線性回歸(multiple linear regression) 是簡單直線回歸的推廣,研究一個因變數與多個自變數之間的數量依存關係。多重線性回歸用回歸方程描述一個因變數與多個自變數的依存關係,簡稱多重回歸。基本信息 多重線性回歸的數學模型為:式中,...
三元線性回歸預測法是指依據三個自變數的變動,來預測因變數發展變化趨勢和水平的方法。計算 回歸方程為:Y=a+bx₁+cx₂+dx₃ 按最小二乘法原理建立方程組:根據已知資料解聯立方程組、 得出a、b、c、d四個參數值、得到具體的...
一元線性回歸分析預測法,是根據自變數x和因變數Y的相關關係,建立x與Y的線性回歸方程進行預測的方法。由於市場現象一般是受多種因素的影響,而並不是僅僅受一個因素的影響。所以套用一元線性回歸分析預測法,必須對影響市場現象的多種因素...
因為Logistic中因變數為二分類變數,某個機率作為方程的因變數估計值取值範圍為0-1,但是,方程右邊取值範圍是無窮大或者無窮小。所以,才引入Logistic回歸。Logistic回歸實質:發生機率除以沒有發生機率再取對數。就是這個不太繁瑣的變換改變...
曲線回歸(curvilinear regression)是指對於非線性關係的變數進行回歸分析的方法。曲線回歸方程一般是以自變數的多項式表達因變數。方法是:根據數據的特點先進行某些變換(如對數變換、平方根變換等),如果變換後得到線性模型,則進行線性回歸...
偏回歸係數是多元回歸問題出現的一個特殊性質。設自變數x1,x2,…,xm與因變數y都具有線性關係,可建立回歸方程:ŷ=b0+b1x1+b2x2+…+bmxm。式中b1,b2,…,bm為相應於各自變數的偏回歸係數。表示當其他的各自變數都保持一定時...
(2)回歸標準差檢驗。計算多元回歸標準差的公式與計算一元線性方程回歸標準差的公式相同,即:式中:yₜ——因變數第t期的觀察值;——因變數第t期的估計值;n——觀察期的個數;k——自由度,為變數的個數(包括因變數和自變數)...
回歸係數(regression coefficient)在回歸方程中表示自變數x 對因變數y 影響大小的參數。回歸係數越大表示x 對y 影響越大,正回歸係數表示y 隨x 增大而增大,負回歸係數表示y 隨x增大而減小。例如回歸方程式Y=bX+a中,斜率b稱為回歸...
在第一個成分被提取後,偏最小二乘回歸分別實施X對t的回歸以及Y對u的回歸。如果回歸方程已經達到滿意的精度,則算法終止;否則,將利用X被t解釋後的殘餘信息以及Y被t解釋後的殘餘信息進行第二輪的成分提取。如此往復,直到能達到一個...
最小二乘法公式是一個數學的公式,在數學上稱為曲線擬合,不僅僅包括線性回歸方程,還包括矩陣的最小二乘法。線性最小二乘法公式為a=y⁻-b*x⁻。矩陣的最小二乘法常用於測量數據處理的平差公式中,VPV=min。簡介 最小二乘法...
