基本介紹
圖書內容,學術貢獻,推理過程,最終結果,學術本質,
圖書內容
學術貢獻
推理過程
李善蘭的尖錐理論,如果用最通俗的語言來表述,就是他首先把一個自然數n用一個平尖錐的圖形來表示,如果這個數是一個平方數,就用一個立尖錐來表示,如果這個數是一個立方數就用一個三乘尖錐來表示,但是,在表示乘方數的時候,尖錐的上面就由平體變成了凹形,乘方越多,凹的就越厲害。 然後,李善蘭把這個尖錐體的乘方數xn用線段來表示,把這個尖錐體迭積成n乘的尖錐面。這種尖錐面由相互垂直的底線、高線和凹向的尖錐曲線組成。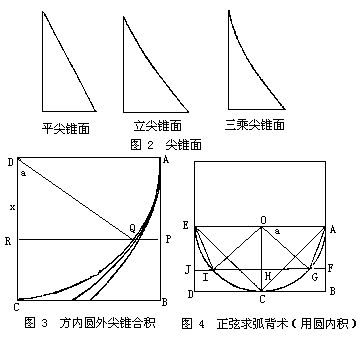 尖錐術現代圖解
尖錐術現代圖解
 尖錐術現代圖解
尖錐術現代圖解最終結果
乘數愈多,也就是說冪次愈高,圓錐曲線的凹就愈甚。 李善蘭在《方圓闡微》中,還採用了一種叫做“分離元數”的方法,歸納出一個二項平方根展開式,然後在四分之一單位圓內套用尖錐術就可以計算出一個方內圓外尖錐的合積,從而獲得圓周率π的無窮級數值。李善蘭創立的尖錐面,是一種處理代數問題的幾何模型。它由互相垂直的底線、高線和凹向的尖錐曲線組成。並且在考慮尖錐合積的問題時,也是使每個尖錐有共同方向的底線和高線。這樣的底線和高線具有平面直角坐標系中的橫、縱兩個坐標的作用。 而且,這種尖錐面是由乘方數漸增漸迭而得。因此,尖錐曲線是由隨同乘方數一起漸增漸迭的底線和高線所確定的點變動而成的軌跡。由於李善蘭把每一條尖錐曲線看作是無窮冪級數中相應的項,這實際上就給出了這些尖錐曲線的代數表示數。  《方園闡幽》書影
《方園闡幽》書影
 《方園闡幽》書影
《方園闡幽》書影
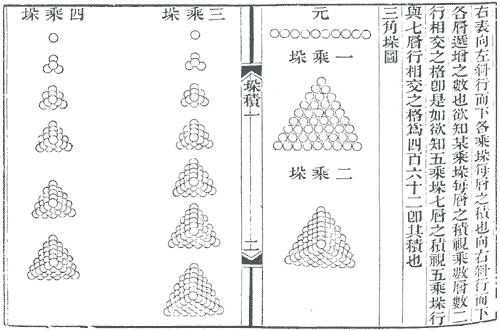 《方園闡幽》書影
《方園闡幽》書影