方嚮導數本質上研究的是函式在某點處沿某特定方向上的變化率問題,梯度反映的是空間變數變化趨勢的最大值和方向。方嚮導數與梯度在微分學中有重要的運用。
基本介紹
- 中文名:方嚮導數與梯度
- 外文名:directional derivative and gradient
- 屬於:數學
- 運用:微積分學、幾何學等
方嚮導數
導數


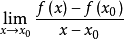
定義
















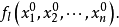
方嚮導數與偏導數、全微分的關係













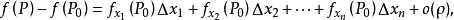


梯度
定義



梯度與方嚮導數的關係




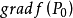




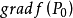




套用


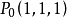


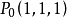



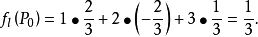




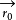



方嚮導數本質上研究的是函式在某點處沿某特定方向上的變化率問題,梯度反映的是空間變數變化趨勢的最大值和方向。方嚮導數與梯度在微分學中有重要的運用。


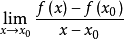
















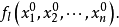













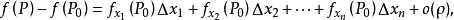









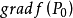




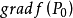






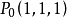


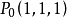



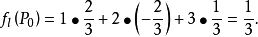






方嚮導數本質上研究的是函式在某點處沿某特定方向上的變化率問題,梯度反映的是空間變數變化趨勢的最大值和方向。方嚮導數與梯度在微分學中有重要的運用。...
在單變數的實值函式的情況,梯度只是導數,或者,對於一個線性函式,也就是線的斜率。梯度一詞有時用於斜度,也就是一個曲面沿著給定方向的傾斜程度。可以通過取向量...
第七節 方嚮導數與梯度 第八節 多元函式的極值及其求法 第九節 二元函式的泰勒公式 第十節 最小二乘法(略) 本章知識結構及內容小結 同步自測題及參考...
方嚮導數……… 72一、多元函式複合求導……… 73二、隱函式的求導公式……… 79三、方嚮導數與梯度……… 85習題6-3 ……… 90第四節 多元函式...
9.7 方嚮導數與梯度9.8 多元函式的極值本章小結第10章 重積分10.1 二重積分的概念與性質10.2 二重積分的計算(一)10.3 二重積分的計算(二)...
過的一些重要概念的圖形特徵的闡述,例如曲線族的包絡線,圖解求導法,平面圖形面積的概念,牛頓—萊布尼茲公式的圖形意義,空間曲面的曲面圖及方嚮導數與梯度的概念的圖形...
第七節 方嚮導數與梯度第八節 多元函式的極值及其求法第九節 二元函式的泰勒公式第十節 最小二乘法(略)本章知識結構及內容小結...
§9 抽象函式二階偏導數的計算§10 含偏導數的等式的證明§11 連續、可偏導和可微之間的關係§12 方嚮導數和梯度的計算§13 多元函式的極值的計算...
§8.6 方嚮導數與梯度§8.7 多元函式的極值及其套用·第8章 多元函式微分法及其套用習題課(二)第9章 重積分§9.1二重積分概念及直角坐標系計算一...
2.2.1 方嚮導數 2.2.2 梯度 2.3 海森矩陣和泰勒展開式 2.3.1 海森(Hesse)矩陣 2.3.2 多元函式的泰勒展開式 習題 第3章 最優性條件 3.1 ...
§8—2偏導數與全微分§8—3多元複合函式求導法則§8—4隱函式求導法則·多元複合函式習題課一§8—5多元函式微分學的幾何套用§8—6方嚮導數與梯度§8—7多元...
偏導數 第三節 全微分 第四節 多元複合函式的求導法則 第五節 隱函式的求導公式 第六節 多元函式微分學的幾何套用 第七節 方嚮導數與梯度 第八節 多元函式的...
3.2 多元函式的偏導數與全微分3.3 方嚮導數與梯度3.4 多元函式的極值問題3.5 多元函式微分學在幾何上的簡單套用3.6 空間曲線的曲率與撓率3.7 多元向量值函式...
習題61*9.8方嚮導數與梯度 619.8.1方嚮導數 619.8.2梯度 63習題64總習題 65第10章重積分 6710.1二重積分的概念及性質 6710.1.1二重積分的概念 67...
9.4.4 複合函式的高階偏導數 習題9.4 9.5 隱函式的微分法 9.5.1 一個方程確定的隱函式 9.5.2 方程組確定的隱函式 習題9.5 9.6 方嚮導數與梯度 9...
8.6方嚮導數與梯度968.6.1方嚮導數968.6.2梯度99習題8.61008.7多元函式微分法在幾何上的套用1018.7.1空間曲線的切線與法平面1018.7.2空間曲面的切平面與法線...
習題7-67.7 方嚮導數與梯度習題7-77.8 多元函式的極值及其求法習題7-8本章小結綜合習題7第8章 重積分8.1 二重積分的概念與性質習題8-1...
8.6 方嚮導數和梯度 628.6.1 基本要求 628.6.2 答疑解惑 628.6.3 基本題型分析 638.6.4 習題全解 658.7?多元函式的極值及套用 678.7.1 基本要求 67...
專題24 方嚮導數與梯度向量及多元函式微分學的幾何套用專題25 重積分專題26 平面上的曲線積分與格林公式專題27 曲面積分與空間中的曲線積分專題28 曲線積分與路徑無...
第二節 數量場的方嚮導數和梯度 1.方嚮導數 2.梯度 習題3 第三節 矢量場的通量及散度 1.通量 2.散度 3.平面矢量場的通量與散度 習題4 第四...
§2.2 方嚮導數與梯度 §2.3 Hesse矩陣及泰勒展式 §2.4 極小點的判定條件 §2.5 錐、凸集、凸錐 §2.6 凸函式 §2.7 約束問題的最優性條件 ...
5 8方嚮導數與梯度170第6章不定積分1756 1不定積分的概念與性質1756 2不定積分的換元積分法1806 3不定積分的分部積分法1886 4幾種特殊類型函式的積分1916...
9.1.9方嚮導數與梯度9.1.10多元函式的極值9.2典型例題分析9.2.1題型一函式定義域及表達式的求解9.2.2題型二二元函式極限的存在性問題...
2.2.1方嚮導數 2.2.2梯度 習題2.2 2.3矢量場的通量及散度 2.3.1通量 2.3.2散度 習題2.3 2.4矢量場的環量及旋度 2.4.1環量 2.4.2旋度 習題2.4 ...
9.4 方嚮導數和梯度 --- 909.4.1 基本要求 --- 909.4.2 基本內容 --- 909.4.3 典型例題 ---...
