基本介紹
- 中文名:拋物線坐標系
- 外文名:Parabolic coordinates
二維拋物線坐標系
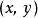








二維標度因子




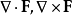

三維拋物線坐標系


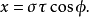




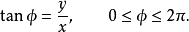









三維標度因子








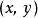












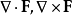



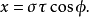




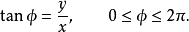

















拋物線坐標系(英語:Parabolic coordinates)是一種二維正交坐標系,兩個坐標的等值曲線都是共焦的拋物線。將二維的拋物線坐標系繞著拋物線的對稱軸旋轉,則可以得到三維...
拋物面坐標系(英語:Paraboloidal coordinates)是一種三維正交坐標系。...... 拋物面坐標系(英語:Paraboloidal coordinates)是一種三維正交坐標系,是二維拋物線坐標系的...
準線、焦點:拋物線是平面內到一定點和到一條不過此點的定直線的距離相等的點的...在平面直角坐標系中作出二次函式y=ax1+bx+c的圖像,可以看出,在沒有特定定義...
拋物柱面坐標系(英語:Parabolic cylindrical coordinates)是一種三維正交坐標系。...... 往 z-軸方向延伸二維的拋物線坐標系,則可得到拋物柱面坐標系。其坐標曲面是共...
拋物線方程是指拋物線的軌跡方程,是一種用方程來表示拋物線的方法。在幾何平面上可以根據拋物線的方程畫出拋物線。拋物線在合適的坐標變換下,也可看成二次函式圖像。...
解:把拋物線拱放到坐標系中去,如圖3所示。易知l=OM =12m,f=KL=2m;代入(4),得拋物線拱的方程為因點B、D、F、H、J都在拋物線拱上,把它們的橫坐標代入...
極坐標系(polar coordinates)是指在平面內由極點、極軸和極徑組成的坐標系。在平面上取定一點O,稱為極點。從O出發引一條射線Ox,稱為極軸。再取定一個單位長度...
平面極坐標系坐標系的一種。極坐標系在平面內由極點、極軸和極徑組成的坐標系。在平面上取一定點o,稱為極點,由o出發的一條射線ox,稱為極軸。對於平面上任意一...
曲面上使兩族參數曲線彼此正交的參數系稱為曲面的正交坐標系。正交坐標系的特徵是其第一基本型的係數F≡0,因此它的第一基型成為I=Edu²+Gdv²。在曲面上...
橢圓拋物面在笛卡兒坐標系中的方程為: [1] 雙曲拋物面在笛卡兒坐標系中的方程...當a = b時,曲面稱為旋轉拋物面,它可以由拋物線繞著它的軸旋轉而成。它是...
頂點坐標是用來表示二次函式拋物線頂點的位置的參考指標,頂點式:y=a(x-h)²+k (a≠0,k為常數)頂點坐標:【-b/2a,(4ac-b²)/4a】。...
周長公式:曲線為開放曲線數學曲線拋物線 直角坐標系標準方程:y^2=2*p*x(x>=0) 極坐標系標準方程:ρ=p/(1-cos(θ))或ρ=e*p/(1-e*cos(θ))(e=1)...
1.拋物線為二次函式的曲線,可以認為是一次函式的曲線即直線的推廣。兩點確定一直線的性質,推廣到拋物線為三點確定一拋物線。(注意:直線的性質和坐標系無關,但...
