基本介紹
- 中文名:拉格朗日鞍點
- 外文名:Lagrange saddle point
- 所屬學科:數學
- 所屬問題:運籌學(非線性規劃)
- 相關概念:拉格朗日函式、非線性規劃等
- 釋義:非線性規劃問題中滿足特定條件的點
基本介紹








鞍點定理



相關概念
非線性規劃



拉格朗日法


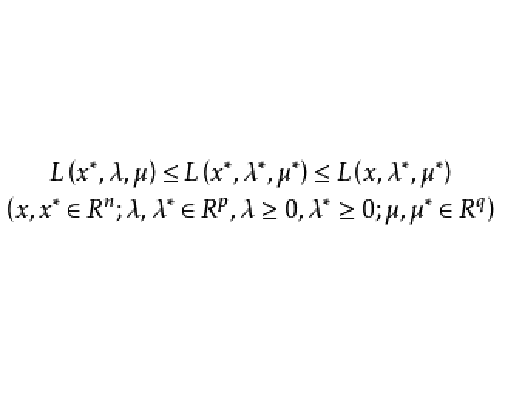
















拉格朗日鞍點(Lagrange saddle point)是非線性規劃問題中滿足特定條件的點。 設(x*,λ*,*μ)是凸最佳化問題的KKT點,則(x*,λ*,*μ)為對應的拉格朗日函式的鞍點,同時也是該凸最佳化問題的全局...
本項研究的目標是將增廣拉格朗日套用到包含數學模型更多的半無限規劃和錐規劃中。具體地, (1) 研究增廣拉格朗日函式在半無限規劃中精確罰參數存在的充分必要條件和鞍點存在的條件。(2) 對廣義半無限規劃建立它的增廣拉格朗日對偶規劃。(3...
對二階錐約束規劃問題得到了其鞍點的存在性。 我們得到了約束最佳化問題的精確罰函式以及增廣拉格朗日乘子存在的二階充分條件. 二. 利用非線性泛函分析方法,臨界點理論,非光滑分析和最佳化等技巧,對橢圓型或拋物型變分不等式和半變分不...
《拉格朗日乘子定理:從一道2005年全國高中聯賽試題的高等數學》是2015-8-1出版的圖書,作者是劉培傑數學工作室編。書名 拉格朗日乘子定理:從一道2005年全國高中聯賽試題的高等數學 作者 劉培傑數學工作室編 ISBN 978-7-5603-5345-6 ...
第5章 lagrange乘子區域分解方法 5.1 基本思想 5.2 乘子空間的構造 5.3 鞍點系統的解法 5.4 算法流程圖 5.5 feti方法 參考文獻 第6章 possion方程的幾何非協調區域分解方法 6.1 模型問題與區域分解 6.2 局部正則化技巧 6.3...
拉格朗日括弧法國數學家和力學家 J.-L.拉格朗日研究正則變換時所用的一種數學符號。拉格朗日括弧是一種與泊松括弧關係密切的運算,1808年至1810年間由約瑟夫·拉格朗日最早用於經典力學之中。不過與泊松括弧相比,拉格朗日括弧已不常使用。定義...
3 拉格朗日對偶性與鞍點最優性 4 算法的基本性質 第三章 最大值原理基本理論 1 時間連續系統最大值原理的若干形式 2 最大值原理的證明 3 最大值原理的證明(泛函分析方法)4 登月艇的軟著陸推力控制問題 5 時間離散系統的最大值...
23 拉格朗日對偶性與鞍點最優性 21 24 算法的基本性質 25 第三章 最大值原理基本理論 31 31 連續時間系統最大值原理的若干形式 31 32 最大值原理的證明 37 33 最大值原理的證明(泛函分析方法) 49 34...
7.4新型的鞍點和相關的結論 第8章多目標規劃的正則牛頓法 8.1引言 8.2約束最佳化問題的內點正則牛頓法 8.3多目標規劃的正則牛頓法 第9章廣義多目標規劃min—max問題及多目標分式規劃的非本質目標函式 9.1廣義min—max問題的熵正則...
