基本介紹
- 中文名:靜電場唯一性定理
- 外文名:The uniqueness theorem
- 套用領域:電磁學
- 相關術語:場強、電勢、邊界條件
定理內容













論證過程








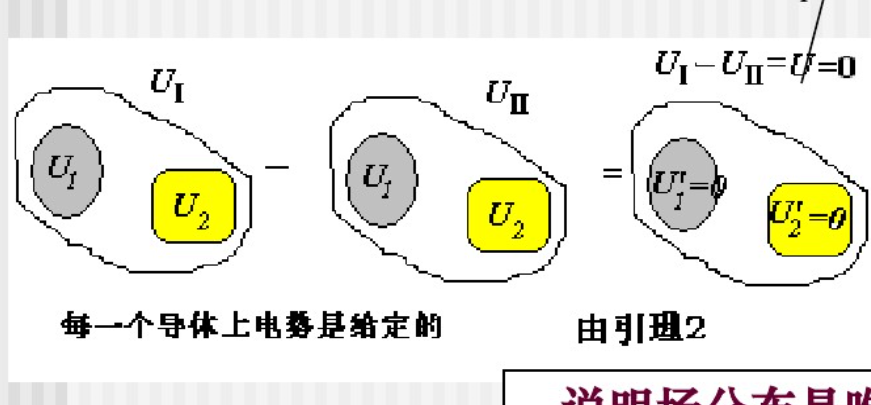





定理的套用
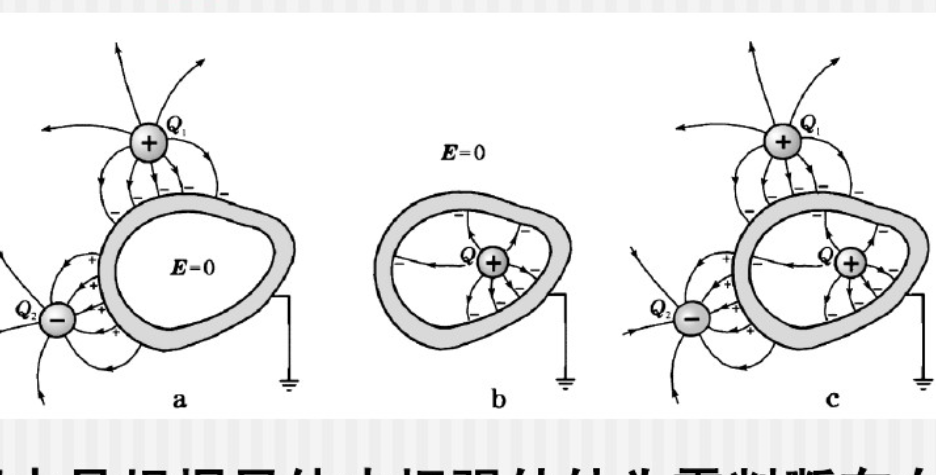
惟一性原理一般指本詞條




























彈性力學惟一性定理是線性彈性力學邊值問題解的定理.該定理斷言:線性彈性體在小位移條件下,其平衡方程列在未變形的物體上,在給定的彈性體上和邊界上的自平衡力系作用下,彈性體內的應變和應力場惟一確定.如果邊界的某區域上給定位移,...
內部惟一性定理是關於解析函式在區域內部由有聚點的子集惟一確定的定理。設D為一區域,在D內定義著兩個單值解析函式,如果這兩個函式在某一集合E⊂D上相等,而E在D內有聚點,則它們在區域D內恆等。用解析延拓定義 設f₁(z)在...
嘉當惟一性定理是單複變函數論中施瓦茲引理的推廣。施瓦茲引理 在單複變函數論中,施瓦茲引理的規範形式為:如果f是單位圓盤到單位圓盤的映射,滿足 那么必有f(z)=z。定義 嘉當(Cartan,H.)把施瓦茲引理推廣到多複變函數,得到所謂的...
對於高維的調和函式,也有與上述類似的最大、最小值原理,平均值公式以及相應的狄利克雷問題解的存在和惟一性定理。一致收斂 一致收斂是高等數學中的一個重要概念,又稱均勻收斂。一致收斂是一個區間(或點集)相聯繫,而不是與某單獨的...
例如有連續的一階和二階偏導數。當自變數為n個(從而區域是n維的)時,則稱它為n維調和函式。對於高維的調和函式,也有與上述類似的最大、最小值原理,平均值公式以及相應的狄利克雷問題解的存在和惟一性定理。
可以歸入這條途徑的還有一種做法,就是引進以有理數為端點的閉區間套原理作為連續性公理的一種替代物。它既比較直觀,同時又避開了十進制無限非循環小數這類一開始難以說清楚的對象,也是一種好方法。惟一性 首先要明白這裡惟一性的確切...
對於高維的調和函式,也有與上述類似的最大、最小值原理,平均值公式以及相應的狄利克雷問題解的存在和惟一性定理。定義 在數學、數學物理學以及隨機過程理論中,都有調和函式的概念。一個調和函式是一個二階連續可導的函式f:U→R(...
時滯泛函微分方程基礎理論,以及作者在解的存在惟一性方面和在邊值問題方面的研究成果;非線性差分方程的基本概念和定理,以及作者在這一領域開展的工作;反應擴散方程的極值原理和比較原理,以及作者在具有元窮時滯的Volterra反應擴散方程...
2.6 惟一性定理62 習題62 第3章 靜電場及其邊值問題的解法64 3.1 靜電場基本方程與電位方程65 3.1.1 靜電場基本方程65 3.1.2 電位定義65 3.1.3 電位方程66 3.2 靜電場中的介質 71 3.2.1 介質的極化71 3....
8.5.1解的存在惟一性定理191 8.5.2擴散過程192 8.5.3簡單例子196 8.6套用——金融衍生產品定價197 8.6.1BlackScholes模型197 8.6.2等價鞅測度199 習題207 第9章Levy過程與關於點過程的隨機積分簡介209 9.1Levy過程209 9...
例如有連續的一階和二階偏導數。當自變數為n個(從而區域是n維的)時,則稱它為n維調和函式。對於高維的調和函式,也有與上述類似的最大、最小值原理,平均值公式以及相應的狄利克雷問題解的存在和惟一性定理。
15.15 常係數線性方程例題選解 15.16 變係數高階線性方程 15.17 例題選解 15.18 列微分方程解套用題 15.19 常係數線性方程組單根的情形 15.20 常係數線性方程組重根的情形 15.21 存在與惟一性定理 附錄 參考文獻 ...
這個條件稱為狄利克雷邊界條件。最主要的問題是證明解的存在性,因惟一性可利用Maximum principle證明。歷史 經典狄利克雷問題以勒熱納·狄利克雷命名,他利用變分方法提出了一個解決辦法,這便是狄利克雷原理。唯一解的存在性由物理分析...
6.4 惟一性 例題 習題 第七章 7 凹規劃 7.1 凹函式及其導數 7.2 凹規劃 7.3 擬凹規劃 7.4 惟一性 例題 習題 第八章 8 二階條件 8.1 局部和全局最大值 8.2 無約束最大化問題 8.3 約束最最佳化 8.4 包絡性質 例題...
技術原理 每個人包括指紋在內的皮膚紋路在圖案、斷點和交叉點上各不相同,呈現唯一性且終生不變。據此,我們就可以把一個人同他的指紋對應起來,通過將他的指紋和預先保存的指紋數據進行比較,就可以驗證它的真實身份,這就是指紋識別...
求得了一類LQ問題的次優解;獲得了部分信息下隨機遞歸系統的最大值原理,得到了本質不同於經典濾波器的濾波方程;構造了由隨機遞歸系統驅動的微分博弈模型,提出了一套研究Nash均衡點存在惟一性的最大值原理方法;探討了股票微分博弈、...
實位拓展定理是數學名詞,實位拓展定理,關於實位拓展的命題.即給出了一個域上的實位在某個實閉包上可以拓展的充分必要條件,同時肯定了拓展的惟一性.定理的存在部分首先由蘭(Lang , S.)獲得,其後,克魯布希(Knebusch , M.)等人...
