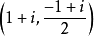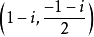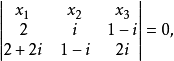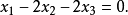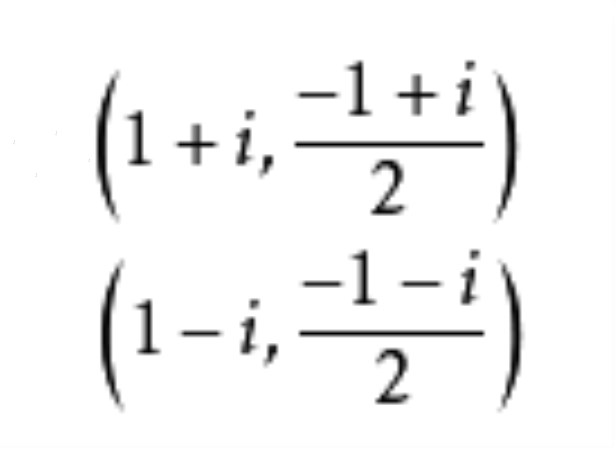復點(complex point)是射影幾何的基本概念之一，指平面上或空間中以複數為坐標的點。復點最初是由於在實空間裡用代數方法研究實曲線的交點等幾何問題時，為求理論上的完整性並便於作統一處理而出現的。在解析幾何中討論二階曲線(或二階曲面)與直線相交的情況時，需解實係數的一元二次方程，這時隨著二次方程有兩個實根、一個重根或兩個虛根，可以確定有兩個交點、一個重合交點(相切情形)或沒有交點(不相交情形)，在研討二階曲線(曲面)以至代數曲線(曲面)時，如果在普通的實平面上(空間中)的點外增添復點，那么這種由於代數方程根的實、虛所反映交點的存在與否的區別就可消失，以至於可以利用每個n次方程總有n個複數根(包括重根)這個代數基本定理來肯定每條直線與任何n次代數曲線(曲面)總有n個交點，這有助於在解析幾何以及代數幾何中對代數曲線(曲面)的理論探討。平面上的復點是這樣定義的：在平面上，若點的坐標x，y皆為實數，則稱(x，y)表示實點；若x，y中至少有一個是虛數，則稱(x，y)表示虛點，實點和虛點合稱為復點。為了表示平面上(空間中)包括無窮遠點在內的全部復點，可對復點引進齊次坐標，這可與實點情形同樣處理。隨著數學的進展和實際的需要而發展起來的復幾何、復空間、複流形等，其基本元素也是復點(複數坐標的點)。
基本介紹
- 中文名：復點
- 外文名：complex point
- 所屬學科：數學
- 所屬問題：高等幾何(射影幾何)
- 簡介：平面上或空間中以複數為坐標的點
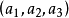
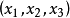
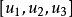
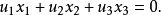
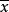
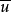
基本概念,相關定理,例題選解,
基本概念
復點，復直線 以複數為坐標的點或直線稱為復點或復直線。
復元素 復點和復直線統稱復元素。
共軛復元素 若
為一元素的齊次坐標時，
為另一同類元素的齊次坐標，則此二元素叫做共軛復元素。
兩個非無窮遠共軛復元素，其非齊次坐標必為共軛複數。
兩個共軛復元素的齊次坐標不一定為共軛複數，原因是齊次坐標可以相差一個常數因子。
復點
和復直線
的結合關係為
相關定理
定理1 一元素為實元素的充要條件是該元素與其共軛復元素重合。
定理2 如果一點x在一直線u上，則共軛復點
必在共軛直線
上。
定理3 兩共軛復直線的交點為一實點，兩共軛復點的連線為一實直線。
推論 在一復直線上有唯一一個實點，過一復點有唯一一條實直線。
注:一實直線上的點或為實點或為一共軛復點；過一實點的直線或為一實直線或為一-共軛復直線。
例題選解
例1 證明：(2，i，1-i)與(2+2i，1-i，2i)表示一對共軛復點，並求其連線方程。
證明： 點(2，i，1-i)之非齊次坐標為
，
點(2+2i，1-i，2i)之非齊次坐標為
。
顯然其坐標為共軛複數，所以此二點為共軛復點，其連線方程為：
例2 (1)求過(1,i,0)之實直線；
(2)求直線[2，i，3-4i)上之實點。
解： (1)通過點(1，i，0)之實直線必過其共軛復點(1，-i，0)，故所求為
。
(2)直線[2，i，3-4i]上之實點為它與共軛復直線[2，-i，3+4i]之交點，故所求為點(-3，8，2)。
