基本介紹
- 中文名:弧長函式
- 外文名:arc length function
- 所屬學科:數學
- 簡介:量度弧長的函式
- 所屬問題:高等數學(微積分)
- 相關方法:微元分析法
基本介紹




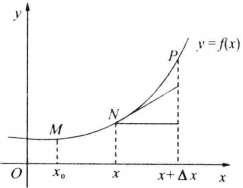
弧長函式的導數和微分







































弧長函式(arc length function),是指量度弧長的函式。設Γ為定義在[a,b]上的可求長曲線,對t∈[a,b],Γ的參數表示φ對[a,t]的限制所表示的曲線的長度記為L(t),如此定義的函式L:[a,b]...
為有界變差函式。特別,微分幾何中考慮的 類曲線(k≥1)都有長度。曲線Γ在[t₀,t]之間的長度可用公式: 表示。弧長稱為曲線的自然參數。在取自然參數時,曲線的方程: 此時,有 ( 表示對弧長s的導矢),反之,若 ,則t可...
利用弧長公式ds=√(1+dy^2/dx^2)*dx;所以s=∫√(1+dy^2/dx^2)*dx 所以把s帶入微分方程得dy/dx=ρ∫√(1+dy^2/dx^2)*dx/H;...(1)對於(1)設p=dy/dx微分處理 得 p'=ρ/H*√(1+p^2)...(...
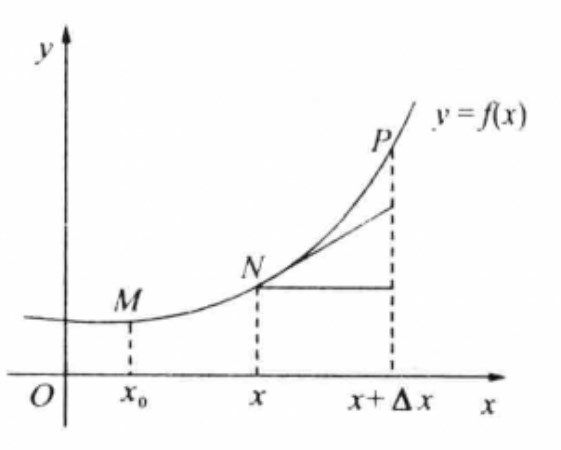
弧微分是用一條線段的長度來近似代表一段弧的長度。設函式f(x)在區間(a,b)內具有連續導數,在曲線Y=f(x)上取定點Mₒ(xₒ,f(xₒ))作為計算曲線弧長的基點,M(x,y)是曲線上任意一點。規定:(1)自變數x增大的方向為...
根據圓的圓心角與圓周弧長的對應關係,可確定:360度角=圓周弧長/半徑=2π弧度 弧度制十分科學,使角與圓弧建立了科學的聯繫,為數算理論的發展、打下了一個堅實的基礎,弧度制角與實數可建立一一對應的關係。角的規定,射線逆時針...
在Matlab,maple等數學軟體中可以直接調用第二類橢圓積分函式求得。建議閱讀《特殊函式》,王竹溪,郭敦仁編著;劉式適、劉式達編著版本指明了第二類橢圓積分的幾何意義即為橢圓弧長問題。外文文獻也很多。十、精確度最高的橢圓周長公式。首...
扇形面積公式描述了扇形面積和圓心角(頂角)、半徑、所對弧長的關係。數學公式表示為:S扇=(lR)/2 (l為扇形弧長) =(1/2)θR²(θ為以弧度表示的圓心角)。公式 設一扇形的半徑為r,弧長為l,面積為s,則 若命扇形的...
的向量函式,常簡寫成分量表示 。三個元素 弧長 設一空間曲線決定於參數方程 式中各函式有直至三階的連續導數,即 。設 是曲線 上的任意點,簡稱 點。是其鄰點。這兩點決定一個向量,即:除以 便得到方向相同而長度不同的向量。當...
曲線論中常討論正則曲線,即其三個坐標函式x(t),y(t),z(t)的導數均連續且對任意t不同時為零的曲線。對於正則曲線,總可取其弧長s作為參數,它稱為自然參數或弧長參數。弧長參數s用 來定義,它表示曲線C從r(α)到r(t)之間的...
3.6弧長微分與曲率 3.6.1弧長函式及其微分 3.6.2曲線的曲率 習題3.6 第4章不定積分 4.1不定積分的概念與性質 4.1.1原函式與不定積分 4.1.2基本積分公式 4.1.3不定積分的基本性質 4.1.4不定積分存在的條件 習題4.1...
在L的取法無關,則稱極限值為f(x,y)在L上對弧長的曲線積分,記為: ;其中f(x,y)叫做被積函式,L叫做積分曲線,對弧長的曲線積分也叫第一類曲線積分。(上述定義並不完全嚴謹,給出新的定義):在矢量場A中,任取一連線點P...
記 s(t)為 t時刻粒子所在位置到曲線上某定點的弧長:由於假設r′ ≠ 0,因此可以將 t表示為 s的函式,因此可將曲線表示為弧長 s的函式 r(s) = r(t(s))。 s通常也被稱為曲線的弧長參數。對於由弧長參數定義的正則曲線 r(...
,n)的n維集合,並且它的曲線xi=xi(t)的“弧長”是按照積分 定義起來的(其中,ρ>0)。這時,稱M為芬斯勒空間。特別是,當 時,得到黎曼空間。P.芬斯勒(1918)在其學位論文中曾經把黎曼空間的一些結果拓廣到這個空間來,但是它的...
為確保過渡段的高度與兩側高度保持一致,過渡段速度與水平方向的速度關係滿足的三角函式關係,與提升量和過渡段弧長的三角函式關係保持一致。組織分析 變壁厚偏心圓環組織較為均勻緻密,壁厚與晶粒尺寸變化趨勢相同。壁厚窄處由於雷射功率低...
在積分學中,橢圓積分最初出現於橢圓的弧長有關的問題中。Guilio Fagnano和歐拉是最早的研究者。通常,橢圓積分不能用基本函式表達。這個一般規則的例外出現在P有重根的時候,或者是R(x,y)沒有y的奇數冪時。但是,通過適當的簡化公式...
《高等數學(第六版)》是由同濟大學數學系編寫,高等教育出版社出版的“十一五”國家級規劃教材、“十二五”普通高等教育本科國家級規劃教材,適合高等院校工科類各專業學生使用。該書分上、下兩冊出版,上冊包括函式與極限、導數與微分、...
《高等數學(第五版)》是由同濟大學數學系編寫,高等教育出版社出版的“十五”國家級規劃教材,可作為工科和其他非數學類專業學生學習高等數學的參考書。該書分上、下兩冊出版,共十二章,上冊內容為函式與極限、導數與微分、中值定理...
上的函式.對曲線 作分割 ,它把分成 個可求長度的小曲線段 , 的弧長記為 ,分割 的細度為 ,在 上任取一點 , 若存在極限 且它的值與分割及點的取法無關,則稱此極限 為 在 上的第一型曲線積分,記為...
曲線論中常討論正則曲線,即其三個坐標函式x(t),y(t),z(t)的導數均連續且對任意t不同時為零的曲線。對於正則曲線,總可取其弧長s作為參數,它稱為自然參數或弧長參數。弧長參數s用 來定義,它表示曲線C從r(α)到r(t)之間的...
