基本介紹
- 中文名:廣義梯度
- 外文名:generalized gradient
- 所屬學科:數學
- 所屬領域:凸分析(凸函式)
- 推出者:克拉克(Clarke,F.H.)
- 類型:數學術語
定義




相關性質


引理1






引理2











定理1

定理2

定理3



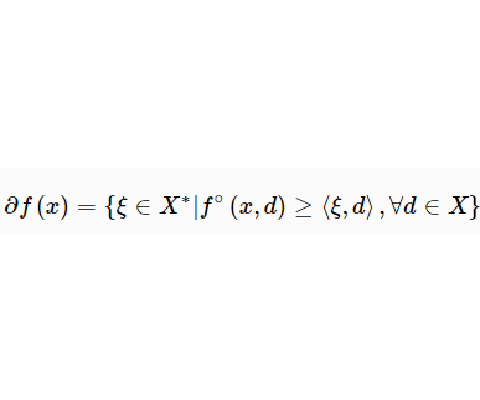




























廣義梯度(generalized gradient)是梯度或導數概念的一種推廣,這是克拉克(Clarke,F.H.)對於局部李普希茨函式類提出的概念,由此形成的理論已成為非光滑分析中最成熟的一部分,並且有廣泛的套用。設f...
狹義梯度推移理論強調區域之間和區域內部的經濟、技術梯度,而忽視了區際和區內社會、自然資源、生態環境、制度、文化等差異形成的梯度。基於這一認識,李國平等提出了“廣義梯度推移理論”。內涵 廣義梯度概念的內涵可用公式表述為:gradΦ=dΦ/dS 其中,gradΦ表示區域梯度水平;分子dΦ表示梯度的硬性或軟性指標,...
《區域經濟協調發展研究--一個廣義梯度理論的分析框架》是2015年科學出版社出版的圖書,作者是李具恆、張美玲。內容簡介 本文以可持續發展為理念,立足多學科與多方法的視角,借鑑國內外已有研究成果,以區域差距與區域經濟協調發展之間的邏輯演進關係為研究的邏輯起點,依據區域經濟發展理論與中國區域經濟發展之間的關聯...
《基於Lojasiewicz不等式的廣義梯度系統大時間行為及套用》是依託哈爾濱工業大學,由薛小平擔任項目負責人的面上項目。項目摘要 常微分方程與偏微分方程所描述的動力系統大時間行為分析是一重要且複雜的問題,尚無統一的處理方法。梯度系統作為特殊的動力系統在數學、物理、力學以及工程計算等領域有廣泛套用,其大時間行為...
具有較高的學術價值。本書可作為高等院校力學、數學、物理,已經工程專業高年級本科生和研究生的教學參考書,亦可供有關教師和科研人員參考使用。圖書目錄 前言 第6章約束力學系統與組合梯度系統 第7章約束力學系統與廣義梯度系統(Ⅰ)第8章約束力學系統與廣義梯度系統(Ⅱ)第9章逆問題的提法和解法 索引 ...
《光滑最佳化》旨在系統介紹非光滑最佳化理論與方法,共分為九章。第1章和第2章分別介紹凸集和凸函式的概念和有關性質;第3章引入凸函式的次微分,給出凸函式的極值條件與中值定理,並介紹次微分的性質和特殊凸函式的次微分表達式;第4章介紹局部Lipscllitz函式的廣義梯度,給出極大值函式廣義Jacobi的計算;第5章闡述...
GGA(generalized gradient approximation)廣義梯度近似。品牌合作商 AMD Kingston AZiO NZXT VisionTek 電競隊伍 職業聯隊 TeamLiquid TeamEZ 受邀請的知名職業玩家 賽事平台 GoSuGamers PlayHem TV 比賽項目 StarCraft II GGA將主辦2012年度星際爭霸 II 的全球電子競技賽, 屆時提供遊戲媒體曝光、重點渠道推廣、新聞媒體...
社會物理學派對於現實問題的探索,通常遵從一定的模式思考,並具較嚴格的邏輯推演,在尋求機制的過程中形成了如下的基本認知框架:(1)承認無論自然系統還是人文系統,無一例外地隨處(空間)隨時(時間)都呈現出“差異”的絕對性;(2)只要存在各種“差異”或“差異集合”,必然產生廣義的“梯度”;(3)只要存在廣義的...
《雷州半島發展研究-基於省域副中心視角》是2019年6月1日中國社會科學出版社出版的圖書,作者是許抄軍。內容簡介 《雷州半島發展研究-基於省域副中心視角》在梳理雷州半島發展歷史脈絡、分析其經濟發展新常態特徵前提下,基於廣義梯度推移理論,首次在不同區域空間比較了湛江的相對梯度水平;基於系統動力學模型,分析了...
《雷州半島發展研究:基於省域副中心視角》是許抄軍創作的經濟學著作,首次出版於2019年6月。該書在梳理雷州半島發展歷史脈絡、分析其經濟發展新常態特徵前提下,基於廣義梯度推移理論,在不同區域空間比較了湛江的相對梯度水平;基於系統動力學模型,分析了湛江的港口優勢;進一步探討了瓊州海峽對半島發展的影響。該書...
非光滑分析(nonsmooth analysis) 是凸分析的發展。凸分析的次微分理論使得人們能夠對非光滑凸函式推廣微分法來處理極值問題。非光滑分析就致力於更一般的廣義微分法,來處理非光滑函式的極值問題。這方面最成功的是克拉克(Clarke,F.H.)對局部李普希茨函式提出的廣義梯度理論,他在1983年出版的《最最佳化和非光滑分析》一...
1、選用12種建立在廣義梯度近似的雜化密度泛函和超級雜化密度泛函,計算研究了N3、N5和N7陽離子的標準生成焓計算,並與報導值對比,修正獲得適合於全氮化合物的理論計算方法。 2、採用廣義梯度近似泛函和6-311+G(d)基組,計算N5陽離子的穩定性以及其與反離子的相互作用,結果可知:N5陽離子在常溫常壓下存在是可能...
wien2k是用密度泛函理論計算固體的電子結構。它基於鍵結構計算最準確的方案——完全勢能(線性)增廣平面波((L)APW)+局域軌道(lo)方法。在密度泛函中可以使用局域(自旋)密度近似(LDA)或廣義梯度近似(GGA)。WIEN 2000使用全電子方案,包含相對論影響。結構功能 X射線結構因子,Baders的“分子中的原子”概念,總...
在構建泛函的過程中,局域密度近似有著重要的地位。基於局域密度近似的泛函是其它更複雜的泛函(如基於廣義梯度近似(GGA)的泛函和雜化泛函)的基礎。一般來說,人們要求所有的泛函都能正確處理均勻電子氣模型,因此所有的泛函中都或多或少地包含局域密度近似項。局域密度近似(LDA)是一種交換關聯能近似。局域密度的概念...
他的重要貢獻包括:交換相關能中的精確絕熱連線形式,導數不連續性及其對能隙的貢獻,線性標度及其對泛函的精確限制條件,密度泛函的自相互作用修正,非經驗的廣義梯度校正近似(GGA),非經驗的meta-GGA泛函。Perdew將DFT的泛函劃分為一系列階梯,提出了Jacob階梯方案,用來設計並提高泛函對交換相關能的描述精度。他在2000...
M.S.穆罕默特等把廣義梯度法和拉格朗日對偶理論結合起來,提出一種統一方法。這種方法具有下列特點:在兩級結構的上下關係方面,控制級(下級)和協調級(上級)的排序是無關緊要的;每一級包含的變數數不受限制;在多台計算機並行工作的情況下,可依據每級計算機的功能適當調配其解題任務。G.科恩在無限維凸規劃(見非...
3.3.2 廣義梯度近似(GGA)3.3.3 廣義梯度近似(GGA)的校正 3.4 贗勢方法 3.5 密度泛函理論的套用 參考文獻 第4章 電子結構研究 4.1 引言 4.2 計算方法和模型的選取 4.2.1 計算方法 4.2.2 計算模型 4.3 結果與討論 4.3.1 計算結果 4.3.2 陽離子摻雜 4.3.3 陰離子摻雜 4.3.4 陰陽...
離子實與價電子之間的相互作用採用全電子投影綴加波(PAW)方法表示,交換關聯作用採用廣義梯度近似(GGA)的Perdew-Burke-Emzerhof(PBE)形式,平面波截斷能採用默認的最大值。在模擬中,採用微正則系綜(NVE),超胞中粒子數目、體積和能量保持不變。時間步長為1fs,總的模擬步數為4000步。HfC超胞結構共含有64個...
實際計算的效果說明,廣義既約梯度法是一種很好的算法。上述線性近似型算法的收斂速度,一般都不高於超線性的。對二階可微的函式ƒ(尣),在尣(k)處若用二次函式·來近似,進而對可微函式ƒ(尣)又用種種變尺度矩陣Hk去代替近似式中的矩陣墷2ƒ(尣(k)),將約束問題的求解化為求一系列二次規劃的解,這...
實際計算的效果說明,廣義既約梯度法是一種很好的算法。上述線性近似型算法的收斂速度,一般都不高於超線性的。對二階可微的函式ƒ(f),在f(k)處若用二次函式·來近似,進而對可微函式ƒ(f)又用種種變尺度矩陣Hk去代替近似式中的矩陣2ƒ(f(k)),將約束問題的求解化為求一系列二次規劃的解,這類方法...
11.(h, φ)-Lipschitz函式及其廣義方嚮導數和廣義梯度 , 數學物理學報, 2006,26(2):212-222 12.一類不完全信息多屬性決策的隨機模擬方法 , 西安電子科技大學學報, 2006,33(2): 287-291 13.區間數互補判斷矩陣排序的一種新方法 , 西安電子科技大學學報, 2006,33(2): 292-294 14.時間最優開光控制的非...
撰有論文《關於廣義梯度的註記》、《可分Banach空間上的局部Lipchitz函式的可微性》、《集值映射的殆半連續性》。貢獻 1979年初,史樹中教授作為公派訪問學者前往法國巴黎法蘭西學院從事研究工作。1981年回國時,他兩年內在《法國科學院報告》上發表了6篇學術論文,其中《關於廣義梯度的幾點註記》一文影響最大,後來又...
