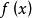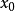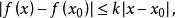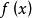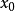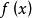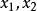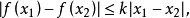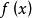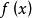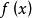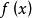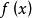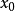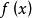李普希茨(Lipschitz,Rudolf Otto Sigismund 1832.5.14—1903.10.7)是德國數學家。生於柯尼斯堡,卒于波恩。1847年入柯尼斯堡大學,不久轉入柏林大學跟隨狄利克雷學習數學,19歲(1851年)時就獲得博十學位。1864年起任波恩大學教授。先後當選為巴黎、柏林、哥廷根、羅馬等科學院的通訊院士。李普希茨在數論、貝塞爾函式論、傅立葉級數、常微分方程、分析力學、位勢理論及微分幾何學等方面都有貢獻。1873年,提出了著名的“李普希茨條件”,對柯西提出的微分方程初值問題解的存在唯一性定理作出改進,得到柯西—李普希茨存在性定理。他的專著《分析基礎》(1877—1880)從有理整數論到函式理論做了系統闡述。在代數數論領域,他引進相應的符號表示法及其計算法則,建立起被稱為“李普希茨代數”的超複數系。在微分幾何方面,他自1869年起對黎曼關於n維流形的度量結構的工作作出進一步闡述和推廣,開創了微分不變數理論的研究,因此被認為是協變微分的奠基人之一。他的工作後來被裡奇有效地用於張量分析。
基本介紹
- 中文名:李普希茨
- 外文名:Lipschitz,Rudolph Otto Sigismund
- 國籍:德國
- 出生地:柯尼斯堡(今加里寧格勒)
- 出生日期:1832年5月14日
- 逝世日期:1903年10月7日
- 職業:數學家
- 簡介:德國數學家、物理學家
- 研究領域:數學分析、數論、微分方程等
基本介紹
李普希茨條件
概念介紹

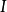
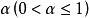
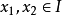
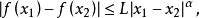

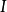
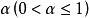

相關分析