集值壓縮映射

集值壓縮映射是一類特殊的集值映射，是在豪斯多夫距離意義下的壓縮映射。

基本介紹

• 中文名：集值壓縮映射
• 外文名：set-valued contraction mapping
• 適用範圍：數理科學

簡介

集值壓縮映射是一類特殊的集值映射，是在豪斯多夫距離意義下的壓縮映射。

集值李普希茨映射

若(X,d)為完備度量空間，CB(X)表示X的所有非空有界閉子集族，δ_X表示CB(X)上的豪斯多夫度量，則(CB(X),δ_X)是度量空間。設(Y,d₁)是完備度量空間，F:X→Y為點有界閉的集值映射。若對於任意x,y∈X，存在常數k使得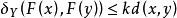

成立，則稱稱F為集值李普希茨映射。

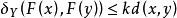
定義

當k<1時，稱F為集值壓縮映射。

當k=1時，稱F為集值非擴展映射。

集值映射

集值映射亦稱多值映射，映射概念的推廣。

設X和Y是兩個集合，記2^Y={A|A⊂Y}，稱之為Y的冪集，從X到Y的一個集值映射指的是從X到2^Y的一個單值映射F：X→2^Y，對於A⊂X，F(A)=∪{F(x)|x∈A}稱為A在F下的像，graph(F)={(x,y)∈X×Y|x∈X,y∈F(x)}稱為F的圖象，任意給定Γ⊂X×Y，則由F(x)={y∈Y|(x，y)∈Γ}(ᗄx∈X)可惟一確定集值映射F：X→2^Y，使得graph(F)=Γ，由F^-1(y)={x∈X|(x,y)∈graph(F)}(ᗄy∈Y)定義的集值映射F^-1：Y→2^X稱為F的逆映射。

壓縮映射

設(X,ρ)為距離空間，T是X到X中的映射，如果存在數a(0<a<1)，使得對所有的x,y∈X都有ρ(Tx,Ty)≤a*ρ(x, y)，則稱T是壓縮映射，壓縮映射也稱為利普希茨映射。