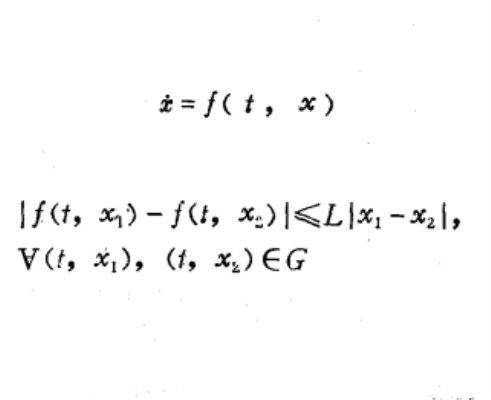李普希茨條件

李普希茨條件(Lipschitz condition)亦稱赫爾德條件，限制函式增量變化大小的一種不等式形式的條件，若f是區間I上的函式，存在正的常數L和α(0<α≤1)，使得只要x₁，x₂∈I，就有|f(x₁)-f(x₂)|≤L|x₁-x₂|^α，則函式f稱為在區間I上滿足α階李普希茨條件，或稱為I上的α階李普希茨函式，記為f∈Lipα(I)或f∈Λ_α(I)。對任意α(0<α≤1)，α階李普希茨函式都是連續函式。特別地，屬於Lip1的函式為絕對連續函式，因而除去一個勒貝格零測度集之外處處可微。一階李普希茨條件是李普希茨(R.(O.S.).Lipschitz)於1864年研究傅立葉級數的收斂判別法時引進的。不少作者把一階李普希茨條件稱為李普希茨條件。1876年，他把它用於微分方程有惟一解問題的討論。0<α<1的α階李普希茨條件其實是赫爾德(O.L.Hölder)引進的，所以又稱為α階赫爾德條件。

基本介紹

• 中文名：李普希茨條件
• 外文名：Lipschitz condition
• 別稱：赫爾德條件
• 所屬學科：數學
• 提出者：李普希茨和赫爾德

基本介紹

1．設 為一函式，k為一正常數，若對於點 之鄰域中的所有點x，都有

則稱 在點 滿足李普希茨條件。

2．設 為定義在 上的函式，k為一正常數， 若對於 中任意兩點 ，都有

則稱 在區間 上滿足李普希茨條件。

若函式 在 上滿足李普希茨條件，則該函式在 上必為絕對連續函式。換言之，絕對連續為李普希茨條件之必要條件，而李普希茨條件為絕對連續的充分條件。

若函式 在 上之任一點均有連續導數，則該函式在 上必滿足李普希茨條件。換言之，有連續導數是李普希茨條件之充分條件，而滿足李普希茨條件是有連續導數的必要條件。

3．設 為一函式，k為一正常數，若對於點 鄰域中的所有點 ，都有

則稱 在點 滿足p次李普希茨條件。

4．設 為定義在 上的函式，k為一正常數， 若對於 上之任意兩點 ，都有

則稱該函式在 上滿足p次李普希茨條件。

顯然，1，2分別是3，4當p=1時的特例。

李普希茨(Lipschitz，1832-1903)是德國數學家，李普希茨條件是他在討論微分方程

解的存在唯一性定理時所引入的。

相關定理

定理1 如果函式 在域G中對t連續，且對變數x滿足李普希茨條件，則它必對 同時連續。 ·

例1 初值問題

試證明微分方程 的右端函式 不滿足對x的李普希茨條件。

證明：如果 滿足李普希茨條件，應有不等式

也即

這意味著在整個定義域中，應是有限的。 然而， 由於時，，因而這是不可能的。所以不滿足李普希茨條件。也正因此， 由微分方程解的存在與唯一性定理可知，儘管右端對x連續，卻並不能保證微分方程的解的唯一性。

現在，我們轉而研究初值問題的解的存在與唯一性定理。

定理2 初值問題解的存在與唯一性定理 如果在某閉域上定義的函式對連續，且對x滿足李普希茨條件，則在t軸上必有一個包含在內的區間，在其中，存在一個滿足微分方程及初始條件的唯一解。

這裡，重要的是指出以下各點：

(1) 如果在某閉域G中，上述微分方程的右端函式對具有有限的偏導數， 即，其中，N為某個常數，則在整個G域中李普希茨條件必可得到滿足。

(2)實際上，滿足李普希茨條件的函式比上述的還要寬廣。例如，微分方程

的右端函式在處不存在偏導數，然而，如果看—下模值情況

顯然，如取李普希茨常數就滿足對x的李普希茨條件了。

(3)儘管滿足李普希茨條件的函式相對講比較寬廣，實用上，為了方便，常把滿足初值問題的解的存在與唯一牲定理的條件取得更窄些。常見的初值問題的存在與唯一性定理表述如下。

定理3 初值問題解的存在與唯一性定理的另一種表達 如果在包括初始點在內的某直角域中，函式和連續，則在中的某域里，必有一個滿足初值問題的唯一解存在。

李普希茨連續映射

李普希茨連續映射(Lipschitz continuousmapping)是滿足李普希茨條件的連續映射。

設有映射 ，若有正常數L，使得

則稱 為李普希茨連續映射，其中正常數L稱為李普希茨常數，(1)式表達的條件稱為李普希茨條件。李普希茨連續映射必是一致連續映射。