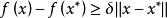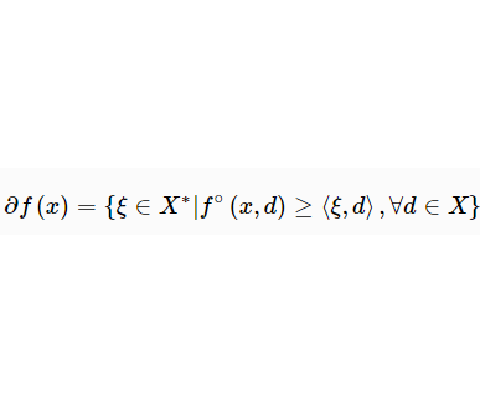廣義梯度

廣義梯度(generalized gradient)是梯度或導數概念的一種推廣，這是克拉克(Clarke，F.H.)對於局部李普希茨函式類提出的概念，由此形成的理論目前已成為非光滑分析中最成熟的一部分，並且有廣泛的套用。設f(x)在x附近是Lipschitz的，則我們稱集合{ξ∈X*|f°(x，d)≥〈ξ,d〉，∀d∈X}是f在x處的廣義梯度，記為∂f(x)。

基本介紹

• 中文名：廣義梯度
• 外文名：generalized gradient
• 所屬學科：數學
• 所屬領域：凸分析（凸函式）
• 推出者：克拉克(Clarke，F.H.)

定義

廣義梯度(generalized gradient)是梯度或導數概念的一種推廣，這是克拉克(Clarke，F.H.)對於局部李普希茨函式類提出的概念，由此形成的理論目前已成為非光滑分析中最成熟的一部分，並且有廣泛的套用。

設f(x)在x附近是Lipschitz的，則我們稱集合

是在處的廣義梯度，記為。

相關性質

共軛空間X*的範數定義為

則關於廣義梯度有如下結果。

引理1

設f(z)在x附近是Lipschitz 的，則

1) 是X* 中的一個弱*—緊的、非空凸集；而且對中任何都有。

2) 關係式

對一切都成立。

根據定義明顯可見廣義方嚮導數和廣義梯度有如下關係。

引理2

設f(z) 在 x 附近是Lipschitz 的，則

若且唯若

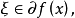
廣義梯度對於數乘具有交換性，即對任何如果是有限個在 x 附近Lipschitz 的函式，則在x附近也是lipschitz 的，而且有關係式

如果每個都在x附近是Lipschitz的，在h(x)附近是Lipschitz的，則f(x)在x 附近是Lipschitz 的且有

其中表示弱*- 緊凸包。

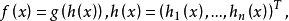
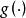
利用引理2，我們可得到非光滑最佳化的一階必要條件：

定理1

如果f(z) 在x* 處達到局部極大或局部極小，且f(x) 在x*附近是Lipschitz 的，則必有

關於充分性條件，我們有以下定理。

定理2

設f(x) 在X* 附近是凸的和Lipschitz 的，且

則x* 是f(x)的局部極小點。

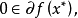
我們還可得到一個關於嚴格(強) 極小點的充分性條件。

定理3

設f(x) 在x*附近是凸的和Lipschitz 的，如果

則x* 是f(x)的嚴格(強)極小點，即存在使得

對所有充分靠近x*點處的x 都成立。