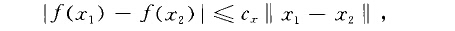
局部李普希茨函式(locally Lipschitz function)一種局部一致的連續函式。
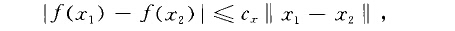
局部李普希茨函式(locally Lipschitz function)一種局部一致的連續函式。設f為巴拿赫空間X的開集,f}CX上的實值函式.如果對於二任門，存在8,‘>。，使得對於任何滿足{}二1一二{} &l...
局部定理 設E為一個完備的有限維賦范向量空間（即一個巴拿赫空間），f為一個取值在E上的函式：其中U為E中的一個開集，I是 中的一個區間。考慮以下的一階非線性微分方程：如果f關於t連續，並在U中滿足利普希茨條件，也就是說，那么對於任一給定的初始條件： ，其中 、 ，微分方程（1）存在一個解 (J,x...
為一函式，k為一正常數，若對於點 之鄰域中的所有點x，都有 則稱 在點 滿足李普希茨條件。2．設 為定義在 上的函式，k為一正常數， 若對於 中任意兩點 ，都有 則稱 在區間 上滿足李普希茨條件。若函式 在 上滿足李普希茨條件，則該函式在 上必為絕對連續函式。換言之，絕對連續為...
利普希茨連續性 利普希茨連續性（Lipschitzian continuity）是1993年公布的數學名詞，出自《數學名詞》第一版。公布時間 1993年，經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
利普希茨條件 利普希茨條件（Lipschitz condition）是1993年公布的數學名詞。公布時間 1993年，經全國科學技術名詞審定委員會審定發布。外文名 Lipschitz condition 出處 《數學名詞》第一版。
利普希茨映射 利普希茨映射（Lipschitzian mapping）是1993年公布的數學名詞。公布時間 1993年，經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
這可能是因為直觀上很難想像一個連續但在不可數個點上不可導的函式。只有對於性質良好的函式，例如利普希茨函式，不可導的點才一定是零測集。魏爾斯特拉斯函式可以說是第一個分形函式，儘管這個名詞當時還不存在。將魏爾斯特拉斯函式在任一點放大，所得到的局部圖都和整體圖形相似。無論如何放大，函式圖像都不會...
1.3 回收函式 18 1.4 函式的回收錐 26 1.5 練習題 30 第2章 閉性準則 32 2.1 關於閉性的討論 32 2.2 線性變換 34 2.3 凸函式的和 48 2.4 練習題 59 第3章 凸函式的連續性 60 3.1 連續性定義 60 3.2 相對邊界上的連續性 63 3.3 利普希茨連續性 69 3.4 凸函式族的連續性 72 3....
函式都是局部利普希茨的，因為局部緊緻空間的連續函式必定有界。性質 符合利普希茨條件的函式一致連續，也連續。bi-Lipschitz函式是單射的。Rademacher定理：若 且 為開集， 符合利普希茨條件，則f幾乎處處可微。 Kirszbraun定理：給定兩個希爾伯特空間， 符合利普希茨條件，則存在符合利普希茨條件的 ，使得 的利普...
就是說，從離散度量空間到另一個有界度量空間的函式是利普希茨連續的，而任何從離散度量空間到另一個有界於1的度量空間的函式是短映射。在其他方向上，從拓撲空間Y到離散空間X的函式f是連續的，若且唯若它是局部常數函式，在所有Y的點都有f在其上的鄰域是常數的意義上。用途 離散結構通常用做不承載任何其他自然...
這可能是因為直觀上想像一個連續但在不可數個點上不可導的函式是很困難的事。當我們繪製函式的圖像時，總會畫出較為規則的圖形，例如滿足利普希茨條件的函式圖像。魏爾斯特拉斯函式可以被視為第一個分形函式，儘管這個名詞當時還不存在。將魏爾斯特拉斯函式在任一點放大，所得到的局部圖都和整體圖形相似。因此，無...
