幾何機率是可以用幾何方法求得的機率。向某一可度量的區域內投一質點,如果所投的點落在門中任意區域 g 內的可能性大小與 g 的度量成正比,而與 g 的位置和形狀無關,則稱這個隨機試驗為幾何型隨機試驗或幾何概型,此處的度量就是測度,一維指長度,二維指面積,三維指體積等。
基本介紹
- 中文名:幾何機率
- 外文名:geometric probability
- 適用範圍:數理科學
簡介

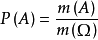




幾何機率是可以用幾何方法求得的機率。向某一可度量的區域內投一質點,如果所投的點落在門中任意區域 g 內的可能性大小與 g 的度量成正比,而與 g 的位置和形狀無關,則稱這個隨機試驗為幾何型隨機試驗或幾何概型,此處的度量就是測度,一維指長度,二維指面積,三維指體積等。

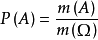



一種機率模型。在這個模型下,隨機實驗所有可能的結果是無限的,並且每個基本結果發生的機率是相同的。例如一個人到單位的時間可能是8:00~9:00之間的任意一個時刻...
幾何機率是可以用幾何方法求得的機率。向某一可度量的區域內投一質點,如果所投的點落在門中任意區域 g 內的可能性大小與 g 的度量成正比,而與 g 的位置和...
藉助於幾何度量計算的機率。 ...... 藉助於幾何度量計算的機率。 [1] 參考資料 1. 鄭家亨,統計大辭典,中國統計出版社,1995年03月第1版,第57頁 V百科往期回顧...
《積分幾何與幾何機率》是世界圖書出版公司出版的圖書,作者是(阿根廷)路易斯桑塔洛。...
幾何分布(Geometric distribution)是離散型機率分布。其中一種定義為:在n次伯努利試驗中,試驗k次才得到第一次成功的機率。詳細地說,是:前k-1次皆失敗,第k次成功...
機率,亦稱“或然率”,它是反映隨機事件出現的可能性(likelihood)大小。隨機事件是指在相同條件下,可能出現也可能不出現的事件。例如,從一批有正品和次品的商品中,...
積分幾何學是通過各種積分考察圖形性質的一門學科,本質上屬於整體微分幾何範疇。積分幾何的研究從歐氏平面和三維歐氏空間開始,逐步拓廣到高維歐氏和非歐空間,然後概括...
《 概型的幾何 》是第1版 (2010年1月1日) 世界圖書出版公司; 出版的圖書...... 《概型的幾何(英文版)》內容簡介:概型理論是代數幾何的基礎,在代數幾何的經...
古典概型也叫傳統機率、其定義是由法國數學家拉普拉斯 (Laplace ) 提出的。如果一個隨機試驗所包含的單位事件是有限的,且每個單位事件發生的可能性均相等,則這個...
英文Geometry一詞,是從希臘語演變而來的,其原意是土地測量、後被我國明朝的徐光啟翻譯成"幾何學"。依據大量實證研究,創造幾何學的是埃及人,幾何學因土地測量而...
《機率論與數理統計》是中國質檢出版社出版的一本圖書,有陳愛江和張文良主編。《機率統計》是高等院校理工類、經管類的重要課程之一。在考研數學中的比重大約占22%...
積分幾何數學中通過各種積分研究圖形性質的一門學科,本質上屬於整體微分幾何範疇。它起源於幾何機率的研究,其發展也始終與幾何機率相聯繫。積分幾何的研究從二維...
《機率初步》是2008年清華大學出版社出版的圖書,作者是陸璇。...... 1.S.2 幾何機率2 隨機變數2.1 離散型隨機變數2.1.1 離散型隨機變數的定義...
機率分布理論是套用機率論和數理統計的原理和方法研究交通特性的一種交通流理論。其立足點是認為車輛行駛屬隨機事件,交通流中的不少特性和參數都是隨機變數,可用各種...
機率決策法則(probabilistic decision rule)是指供選擇的備選方案因不可控制因素呈機率變化條件下的決策規則。通過計算可得知備選方案發生或不發生的機率的大小,經過...
機率圖模型是用圖來表示變數機率依賴關係的理論,結合機率論與圖論的知識,利用圖來表示與模型有關的變數的聯合機率分布。由圖靈獎獲得者Pearl開發出來。機率圖模型...
《幾何VS代數》是名校名師特別奉獻給高中學子的一篇名作,將新課標高中數學的超重要公式定理特別整理在前,並按知識邏輯大致劃分成高一、高二、高三三個學段,便於學生...
屬於礦山測量學和採礦學的一個分支。指用圖解和分析等方法,研究礦體的空間幾何形態、埋藏條件以及礦產質量的分布和變化規律,以解決礦床勘探和開採中有關問題的一門...
機率指事件隨機發生的機率,對於均勻分布函式,機率密度等於一段區間(事件的取值範圍)的機率除以該段區間的長度,它的值是非負的,可以很大也可以很小。...
