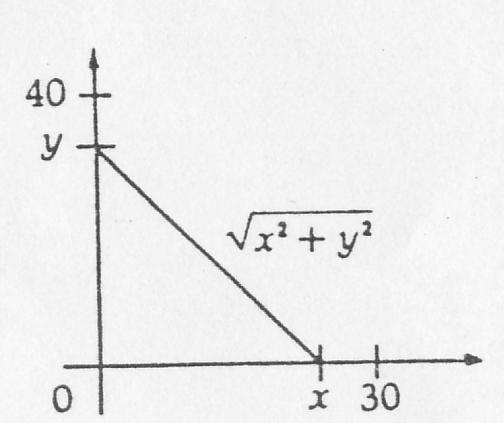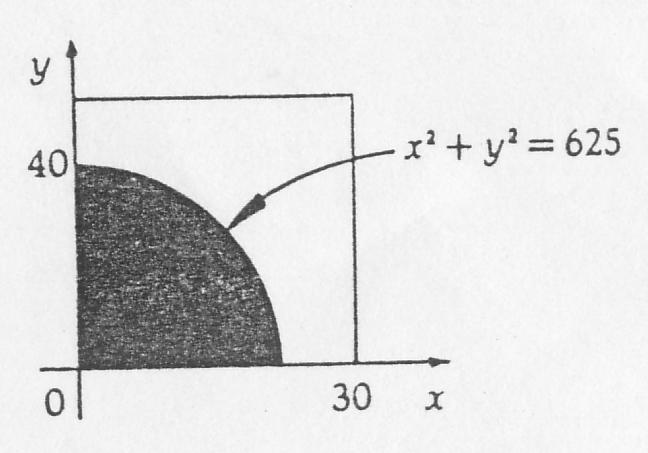定義
如果每個事件發生的
機率只與構成該事件區域的長度(面積或體積或度數)成比例,則稱這樣的機率模型為幾何機率模型,簡稱為幾何概型。
比如:對於一個隨機試驗,我們將每個基本事件理解為從某個特定的幾何區域內隨機地取一點,該區域中每一個點被取到的機會都一樣;而一個
隨機事件的發生則理解為恰好取到上述區域內的某個指定區域中的點。這裡的區域可以是
線段,
平面圖形,
立體圖形等。用這種方法處理
隨機試驗,稱為幾何概型.
幾何概型與
古典概型相對,將
等可能事件的概念從有限向無限的延伸。這個概念在我國國中數學中就開始介紹了。
古典概型與幾何概型的主要區別在於:幾何概型是另一類等可能概型,它與古典概型的區別在於試驗的結果是無限個。
特點
幾何概型的特點有下面兩個:
(1)無限性:試驗中所有可能出現的基本事件(結果)有無限多個.
(2)等可能性:每個基本事件出現的可能性相等.
計算公式
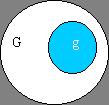
設在空間上有一區域
G,又區域
g包含在區域
G內(如圖),而區域
G與
g都是可以度量的(可求面積),現隨機地向
G內投擲一點
M,假設點
M必落在
G中,且點
M落在區域
G的任何部分區域
g內的機率只與g的度量(長度、面積、體積等)成正比,而與
g的位置和形狀無關.具有這種性質的隨機試驗(擲點),稱為幾何概型。關於幾何概型的隨機事件“ 向區域
G中任意投擲一個點
M,點
M落在
G內的部分區域
g”的
機率P定義為:
g的度量與
G的
度量之比,即
P=g的測度/G的測度
幾何概型求事件A的機率公式:
一般地,在幾何區域D中隨機地取一點,記事件“該點落在其內部一個區域d內”為事件A,則事件A發生的機率為:
P(A)=構成事件A的區域長度(面積或體積)/ 實驗的全部結果所構成的區域長度(面積或體積)
這裡要指出:D的測度不能為0,其中“測度”的意義依D確定.當D分別為線段,平面圖形,立體圖形時,相應的“測度”分別為長度,面積,體積等.
例題詳解
例1 磁帶問題
喬和摩進行了一次關於他們前一天夜裡進行的活動的談話。然而談話卻被監聽錄音機記錄了下來,磁帶長30分鐘。聯邦調查局拿到磁帶並發現其中有10秒鐘長的一段內容包含有他們倆犯罪的信息,然而後來發現,這段談話的一部分被聯邦調查局的一名工作人員擦掉了,該工作人員聲稱她完全是無意中按錯了鍵,並從即刻起往後的所有內容都被擦掉了,試問如果這10秒鐘長的談話記錄開始於磁帶記錄後的半分鐘處,那么含有犯罪內容的談話被部分或全部偶然擦掉的機率將是多大?
解:將30分鐘的磁帶表示為長度為30的線段R,則代表10秒鐘與犯罪活動有關的談話的區間為r,10秒鐘的談話被偶然擦掉部分或全部的事件僅在擦掉開始的時間位於該區間內或始於該區間左邊的任何點。 因此事件r是始於R。
線段的左端點長度為1/2+1/6=2/3的事件。因此有
P(
r)=(
r的長度)/(
R的長度)=(2/3)/30=2/90=1/45
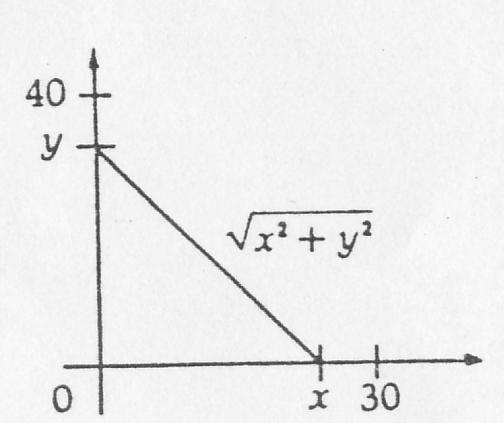
答:含有犯罪內容的談話被部分或全部偶然擦掉的機率將是1/45。
例2 CB對講機問題
兩個CB(CB即Citizen Band市民波段的英文縮寫)對講機持有者,莉莉和霍伊都為卡爾貨運公司工作,他們的對講機的接收範圍為25公里,在下午3:00時莉莉正在基地正東距基地30公里以內的某處向基地行駛,而霍伊在下午3:00時正在基地正北距基地40公里以內的某地向基地行駛,試問在下午3:00時他們能夠通過對講機交談的機率有多大?
解:設
x和
y分別代表莉莉和霍伊距某地的距離,於是0≤
x≤30,0≤
y≤40。則他倆所有可能的距離的數據構成有序點對(
x,
y),這裡
x,
y都在它們各自的限制範圍內,則所有這樣的有序數對構成的集合即為基本事件組對應的幾何區域,每一個幾何區域中的點都代表莉莉和霍伊的一個特定的位置,他們可以通過對講機交談的事件僅當他們之間的距離不超過25公里時發生(如右上圖),因此構成該事件的點由滿足不等式(
x^2+
y^2)≤25^2的數對組成,此
不等式等價於
x^2+
y^2≤625。
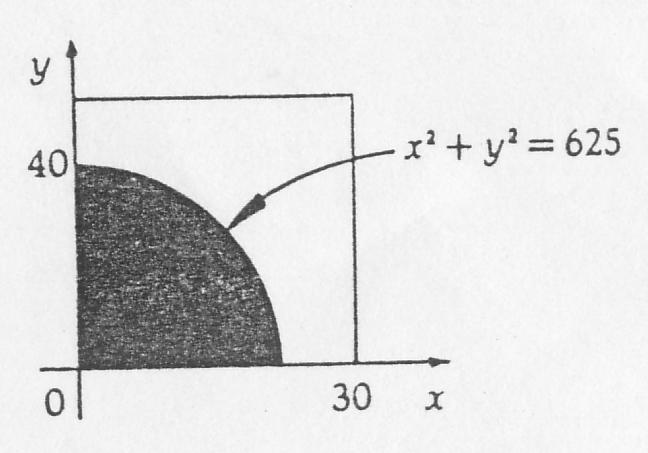
右圖中的方形區域代表基本事件組,陰影部分代表所求事件,方形區域的面積為1 200平方公里,而事件的面積為(1/4)π(25)^2=625π/4。
於是有P=(625π/4)/1 200=625π/4 800=0.41。
答:在下午3:00時他們能夠通過對講機交談的機率是0.41