基本介紹
- 中文名:平面向量數量積
- 外文名:Scalar product of plane vector
- 所屬學科:數學
- 所屬領域:幾何學
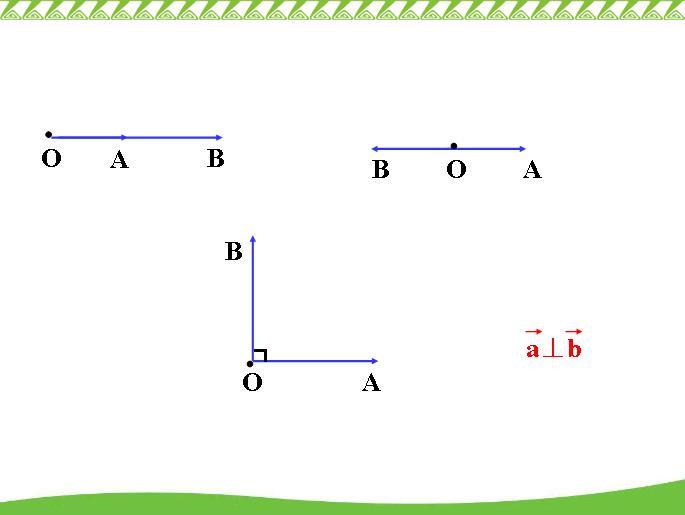
已知兩個非零向量a、b,那么|a||b|cosθ(θ是a與b的夾角)叫做a與b的數量積或內積。記作a·b。兩個向量的數量積等於它們對應坐標的乘積的和。即:若a=(x₁,y₁),b=(x₂,y₂),則a·b=x₁·x₂+y...
主要是從投影的角度理解平面向量的數量積的幾何意義,並解決簡單問題。設計思路 本節課的設計分為3個環節,首先通過引例得到平面向量數量積的幾何意義,再利用數量積的幾何意義解決簡單問題,最後進行利用幾何意義解決問題的方法小結。
平面向量是在二維平面內既有方向(direction)又有大小(magnitude)的量,物理學中也稱作矢量,與之相對的是只有大小、沒有方向的數量(標量)。平面向量用a,b,c上面加一個小箭頭表示,也可以用表示向量的有向線段的起點和終點字母表示。...
平面向量的數量積a·b是一個非常重要的概念,利用它可以很容易地證明平面幾何的許多命題,例如勾股定理、菱形的對角線相互垂直、矩形的對角線相等等。如證明:(1)勾股定理: Rt△ABC中,∠C=90°,則|CA|²+|CB|²=|AB|...
兩個非零向量的數量積:。數量積滿足交換律、分配律,不滿足結合律。充要條件 向量平行(共線)充要條件的兩種形式:(1) ;(2) 。比較 共線向量與平行向量關係 由於任何一組平行向量都可移到同一直線上,故平行向量也叫做共線...
第一講平面向量及其運算 1.1平面向量的實際背景及基本概念 1.2平面向量的線性運算(Ⅰ)——向量的加減法運算及其幾何意義 1.3平面向量的線性運算(Ⅱ)——向量的數乘與平面向量基本定理 1.4平面向量的數量積 高考熱點題型評析與...
向量積可以被定義為:模長:(在這裡θ表示兩向量之間的夾角(共起點的前提下)(0°≤θ≤180°),它位於這兩個矢量所定義的平面上。)方向:a向量與b向量的向量積的方向與這兩個向量所在平面垂直,且遵守右手定則。(一個簡單的...
第6課 平面向量的數量積 第7課 平面向量的綜合套用 第3篇 解三角形與複數 第8課 正弦定理與餘弦定理 第9課 解三角形問題及其簡單套用 第10課 複數與算法 參考答案 作者簡介 王懷學,中國教育學會會員,江蘇省考試專業委員會常務...
一、向量的坐標表示(9題)二、向量的夾角(16題)三、向量的模(4題)四、綜合題(11題)第九節平面向量的數量積 一、數量積的定義(22題)二、數量積的坐標表示(13題)三、綜合題(5題)第十節平面向量的綜合套用 一、向量...
4.專題探究 4.1 案例精講 4.2 探究測試 5.專題視野 5.1 史海拾遺 5.2 套用平台 專題三 平面向量的數量積 專題四 向量的套用舉例 專題五 程式框圖與算法語句 專題六 算法案例 綜合測試(一)綜合測試(二)參考答案 ...
第6章 平面向量 6.1 平面向量及其線性運算 6.1.1 平面向量的概念 6.1.2 平面向量的線性運算 6.2 平面向量的坐標表示 6.2.1 平面向量的直角坐標 6.2.2 向量線性運算的坐標表示 6.3 平面向量的數量積 6.3.1 平面向量的...
9.4.2 平面向量數量積的坐標表示 第十章 三角恆等變換與解三角形 10.1 兩角和與差的正弦、餘弦與正切公式 10.2 倍角公式 10.2.1 倍角公式 10.2.2 簡單的三角恆等變換 10.3 解三角形 ...
2.4.1平面向量數量積的物理背景及其含義 2.4.2平面向量數量積的坐標表示、模、夾角 2.5平面向量的套用舉例 2.5.1平面幾何中的向量方法 2.5.2向量在物理中的套用舉例 第三章三角恆等變換 3.1兩角和與差的正弦、餘弦和正切公式...
1平面向量數量積 2平面向量數量積的性質及其坐標表示 3平面向量的數量積的運算律 4平面向量數量積的運算 5向量的垂直與夾角問題 6平面向量的套用 7有關向量數量積的綜合問題 能力測試點24 正弦定理和餘弦定理及其套用 1正弦定理 2餘弦...
導師·導學向量的數量積和數乘的區別與聯繫/111 考點2數量積的性質及其運算律/113 考點3 兩向量的夾角/114 考點4數量積的套用/115 拓展·研討如何利用向量方法解三角函式/116 2.4.2平面向量數量積的坐標表示 考點1 平面向量數量積...
8.4平面向量的數量積 8.5平面向量套用舉例 第九章三角恆等變換 9.1兩角和與差的正弦、餘弦和正切公式 9.2簡單的三角恆等變換 第十章解三角形 10.1正弦定理和餘弦定理 10.1.1正弦定理 10.1.2餘弦定理 10.2套用舉例 第十一章...
11.4.2 平面向量數量積的坐標表示 11.5 向量在平面幾何中的套用 11.6 向量與平面解析幾何 11.6.1 直線的點方向式方程 11.6.2 直線的點法向式方程 11.6.3 直線的斜率和傾斜角 11.6.4 兩直線的夾角 11.6.5 點到直線的...
2.4平面向量的數量積 2.5平面向量套用舉例 單元專題提升 第二章單元學能測評 第三章三角恆等變換 3.1兩角和與差的正弦、餘弦和正切公式 3.2簡單的三角恆等變換 單元專題提升 第三章單元學能測評 測評參考答案 ...
2.4 平面向量的數量積 2.5 平面向量的套用舉例 第三章 三角恆等變換 3.1 兩角和與差的正弦、餘弦和正切公式 3.2 簡單的三角恆等變換 必修5 第一章 解三角形 1.1 正弦定理和餘弦定理 1.2 套用舉例 第二章 數列 2.1 數列...
一平面向量數量積的概念91 二數量積的幾何意義92 三平面向量數量積的性質92 四平面向量數量積的運算律93 五平面向量數量積的坐標表示94 六向量運算中的最值問題95 七利用向量的數量積解決平面幾何問題96 八向量的夾角及垂直問題的求解...
(考點) 1 平面向量數量積的運算及幾何意義 2 與向量模有關的計算 3 兩向量的夾角問題 4 平面向量的垂直問題 第5節 平面向量套用舉例 (考點) 1 向量在平面幾何中的套用 2 向量在解析幾何中的套用 3 向量在物理中的套用 本章...
1.4 平面向量的數量積 1.5 平面向量的套用舉例 專題一 向量的運算 專題二 共線問題 專題三 求向量的模(長度)專題四 向量的夾角與垂直問題 專題五 向量在判斷幾何圖形形狀中的套用 專題六 向量與代數 專題七 向量與三角 專題八 ...
2.4 平面向量的數量積 2.5 平面向量套用舉例 閱讀與思考 向量的運算(運算律)與圖形性質 小結 複習參考題 第三章 三角恆等變換 3.1 兩角和與差的正弦、餘弦和正切公式 信息技術套用 利用信息技術製作三角函式表 3.2 簡單的...
5.2平面向量的數量積及套用舉例一 考點1 平面向量的數量積 者點2平面向量的套用 5.3數系的擴充與複數的引入 者點1複數的概念 考點2複數的代數運算 考點3複數的幾何意義 專題二三角與向量 第六章數列 6.1數列的概念 考點1數列的...
2.4.1 平面向量數量積的物理背景及其含義 2.4.2 平面向量數量積的坐標表示、模、夾角 2.5 平面向量套用舉例 本章知識整合 第三章 三角恆等變換 本章學習思路 3.1 兩角和與差的正弦、餘弦和正切公式 3.1.1 兩角差的...
2.3 平面向量的數量積 2.4 平面向量套用舉例 章節測試 第三章空間向量與立體幾何(選學)3.1 空間向量及其運算 3.2 立體幾何中的向量方法 章節測試 第四章數系的擴充與複數的引入(選學)4.1 數系的擴充和複數的概念 4.2 複數...
《高中數學-新陽光專題攻略》是2007年北京出版社出版的圖書,作者是新陽光專題攻略編委會。內容介紹 《新陽光專題攻略:高中數學(平面向量與平面解析幾何)》內容涉及:平面向量、直線與線性規劃、圓與圓錐曲線,對其中平面向量的數量積運算和...
第8章 平面向量 8.1 平面向量的概念 1.向量的概念 2.共線向量 習題 8.2 向量的線性運算 1.向量的加法 2.向量的減法 3.向量的數乘 習題 8.3 向量的坐標運算 1.位置向量 2.向量的坐標表示 3.向量平行的坐標表示 4...
第二章 面向量 2.1 平面向量的實際背景及基本概念 2.2 平面向量的線性運算 2.3 平面向量的基本定理及坐標表示 2.4 平面向量的數量積 2.5 平面向量套用舉例 單元測試 第三章 角恆等變換 3.1 兩角和與差的正弦、餘弦和正切公式...
9.4 向量的數量積 9.4.1 平面向量數量積的含義 9.4.2 平面向量數量積的坐標表示 9.5 向量的套用 第九章綜合測試 第十章 複數 10.1 數系的擴充 10.2 複數的幾何表示 10.3 複數的四則運算 10.3.1 複數的加法和...
