基本介紹
- 中文名：局部道路連通空間
- 外文名：Local road connecting space
- 學科：數學
- 性質：拓撲空間
- 定義：設X為拓撲空間，對 ，如果X在x處是局部道路連通的，則稱X為局部道路連通空間
- 相關名詞：局部道路連通
簡介,定義,相關定義,推論,相關概念,連通空間,局部連通空間,道路連通空間,
簡介
定義
設X為拓撲空間，對
，如果X在x處是局部道路連通的，則稱X為局部道路連通空間。
相關定義
（1）設X為拓撲空間，
分別為
的鄰域系與鄰域基，如果對
，V是X的道路連通子集，則稱
為
的道路連通鄰域基，簡稱 為 的道路連通鄰域基。
（2）設X為拓撲空間，如果對
，V是X的道路連通子集，存在 的道路連通鄰域V，使得
，則稱X在 處是局部道路連通的。
推論
（1）拓撲空間X在 是局部道路連通的若且唯若X在 處存在道路連通鄰域基。
（2）X是局部道路連通空間若且唯若對 ，都存在x的道路連通鄰域基。
證明：根據上述定義及推論，拓撲空間x是局部道路連通空間等價於對 ，X在x處是局部道路連通的。等價於 對 ，存在x的道路連通鄰域基。
（3）實數空間R是局部道路連通空間。
證明：對
，則x的所有球形鄰域構成的集族 為x的鄰域 基。又因為R中的球形鄰域都是道路連通的 開區間，所以 為x的道路連通鄰域基。由上述定義和推論得，R為局部道路連通空間。
（4）局部道路連通空間必為局部連通空間。
證明：設x是局部道路連通空間，由上述定 義和推論得，對 ，存在x的道路連通鄰域基 ，使得對
，滿足 ，因為v是道路連通的，因而也是連通的，所以 是 x 的連通鄰域基，因此X是局部連通空間。
（5）設C是拓撲空間x的一個道路連通分支，Y為x的道路連通子集，並且
，則
包含於C。
證明：因為 ，故任取
，對任意y∈Y， 由於Y是X的道路連通子集，而x,y∈Y，所以x與 y是道路連通的，因而x與y屬於x的同一個道路連通分支，又x∈C，C是x的道路連通分支，從而y∈C，所以Y包含於C。
（6）道路連通分支是拓撲空間中最大的道路連通子集。
（7）設X為拓撲空間，Q為X的基，如果Q中每個成員都是道路連通，則稱Q為X的道路連通基。
（8）設X為拓撲空間，則下列條件等價：
- X 是局部道路連通空間；
- X 任意開集的任意道路連通分支都是開集；
- X 有一個道路連通基；
- 對所有的x∈X，存在 x 的道路連通鄰域基。
（9）局部道路連通空間的每一個道路連通分支都是開集。
（10）設X為局部道路連通空 間，Y為拓撲空間，
為連續滿的開映射,則Y是局部道路連通空間。
（11）局部道路連通性是拓撲不變性質。
（12）局部道路連通性是有限可積性質。
（13）n維歐氏空間
是局部道路連通空間。
（14）局部道路連通空間的每一個開子空間都是局部道路連通空間。
證明：設X是局部道路連通空間，U為X的任意開集，V為U的任意開子集，則V也是X的開集，由定理，V的每一個道路連通分支都是X的開集，故V的每一個道路連通分支也是V的一個開集，從而V的每個道路連通分支也是U 的一個開集，U是X的局部道路連通開子空間。
（15）局部道路連通性對開子空間是可遺傳的。
（16）設X是局部道路連通空間，則X是連通空間若且唯若X是道路連通空間，並且X只有一個連通分支，也是它的道路連通分支，此分支為X。
證明：設X是局部道路連通空間，由於X是自身的開子集，根據定理，x是連通空間等價於X是道路連通空間， X為連通空間只有一個道路連通 支，這個道 路連通分支也是X的連通分支，即此分支為X，連通空間與道路連通 空間，局部連通空間與局部道路連通空間，連通分支與道路連通分支以及n維歐氏空間 之間的關係框圖如下：
局部道路連通空間關係框圖
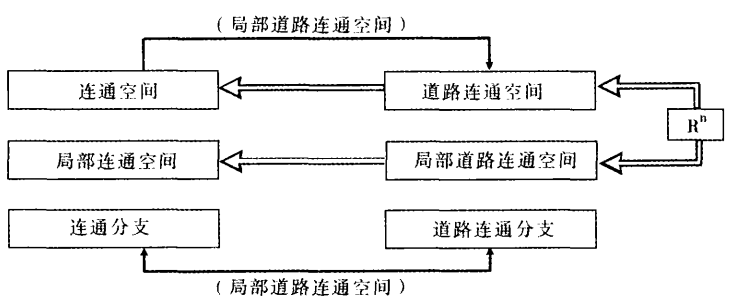
相關概念
連通空間
設X是一個拓撲空間。如果X中有兩個非空的隔離子集A和B，使得X= A∪ B，則稱X是一個不連通空間；否則，則稱X是一個連通空間。
局部連通空間
設X是一個拓撲空間。如果x∈ X的每一個鄰域中都包含著x的某一個連通的鄰域V，則稱拓撲空間在點x處是局部連通的。如果拓撲空間X在它的每一個點處都是局部連通的，則稱是一個局部連通空間。
局部連通的拓撲空間也不必是連通的。例如，每一個離散空間都是局部連通空間，但包含著多於一個點的離散空間卻不是連通空間。又例如，n維歐氏空間的任何一個開子空間都是局部連通的(這是因為每一個球形鄰域都同胚於整個歐氏空間，因而是連通的)，特別地，歐氏空間本身是局部連通的。另一方面，歐氏空間中由兩個無交的非空開集的並作為子空間就一定不是連通的。
此外根據定義立即可見：拓撲空間X在點x∈X處是局部連通的若且唯若x的所有連通鄰域構成點二處的一個鄰域基。
道路連通空間
設X是一個拓撲空間，如果對於任何x, y，存在著X中的一條從x到y的道路(或曲線)，我們則稱X是一個道路連通空間。X中的一個子集Y稱為X中的一個道路連通子集，如果它作為X的子空間是一個道路連通空間。
實數空間R是道路連通的，這是因為如果x, y∈R，則連續映射f： [0,1]
R定義為對於任何t∈[0,1]有f(t)=x+t(y-x)，便是R中的一條以x為起點以y為終點的道路。也容易驗證任何一個區間都是道路連通的。
