坐標反算

坐標反算是指根據直線的起點和終點的坐標，計算直線的水平距離和坐標方位角的過程。坐標反算一般主要套用於測繪工程、建設工程之中，具體在建築設計，工程測量，測繪製圖等領域。總的來說坐標計算分為坐標正算和坐標反算兩種，這兩種在實際中是較常見的。

基本介紹

• 中文名：坐標反算
• 外文名：Inverse calculation of coordinate
• 性質：科學
• 類別：數學

定義

坐標反算

根據已知直線的起點和終點坐標，來計算直線的水平距離和坐標方位角的過程叫坐標反算。

坐標正算

根據直線的起點坐標、直線的水平距離以及坐標方位角來計算終點的坐標的過程叫坐標正算。

計算原理

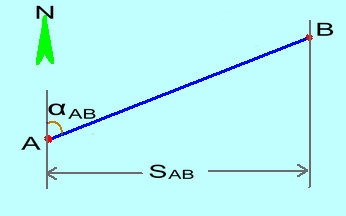
如圖中所示，已知一條直線的起點和終點坐標分別為A點坐標（XA, YA）,B點坐標（XB, YB）,A點到B點距離L,A點到B點方位角aAB，通過坐標反算來計算直線AB的水平距離S ab和坐標方位角α ab。

坐標正算公式： XB=XA+LcosaAB

YB=YA+LsinaAB

坐標反算公式：L^2= (XB-XA)^2+（YB-YA）^2

由於反三角函式計算的結果有多值性所以在計算坐標方位角α ab之前，要先計算象限角R ab。

計算步驟

①tan R ab=|△y ab|╱|△x ab|=|y b-y a|╱|x b-x a|；

②R ab=arctan|y b-y a|╱|x b-x a|；

③L=|△y ab|╱sinα ab=|△x ab|╱cosα ab。Sab=△y ab。L是A、B兩點間距離，Sab是水平距離。

④根據“②”中所求的R ab，求坐標方位角α ab，

⑴若坐標方位角為第一象限角，則：R ab=α ab；

⑵若坐標方位角為第二象限角，則：α ab=180°-R ab；

⑶若坐標方位角為第三象限角，則：α ab=180°+R ab；

⑷若坐標方位角為第四象限角，則：α ab=360°-R ab。

附註

坐標方位角：直線的方向是用方位角來表示的，其中以坐標北方向為基準方向，順時針旋轉到直線的水平角度，稱為該直線的坐標方位角。

象限角劃分：第一象限角：0°~90°

第二象限角：90°~180°

第三象限角：180°~270°

第四象限角：270°~360°

另注意：此象限角的劃分與數學中的象限角不同，應注意！

現場確定坐標系

如果找到兩個基準點A(N3000,E4500,Z100), B(N2900,E5500,Z120)，則可以根據基準點坐標值反推坐標系，找到N,E方向。

首先確定N,E方向：

從E坐標可以發現，B點E坐標大於A點，所以B點應在A點的東面。再看B的N坐標小於A點，故B點應在A點南面。即B點在A點東南面。

求出直線AB與E坐標的夾角：

a=atg((Nb-Na)/(Eb-Ea))

-90degree<=a<=90degree

若a>0，則直線從A到B成右上方向走向。若a<0，則直線從A向B成左下方向走向。若a=0，則AB平行於E軸線。若a=+90或-90度，則直線垂直於E軸線。由此可以確定現場的NE坐標系。