嚴格偏序關係(strictly partially ordered relation)是一種重要的偏序關係,集合X上的關係R若具有反自反性和傳遞性,則稱R為X上的一個嚴格偏序,記作<。
基本介紹
- 中文名:嚴格偏序關係
- 外文名:strictly partially ordered relation
- 所屬學科:數學(集合論)
- 簡介:一種重要的偏序關係
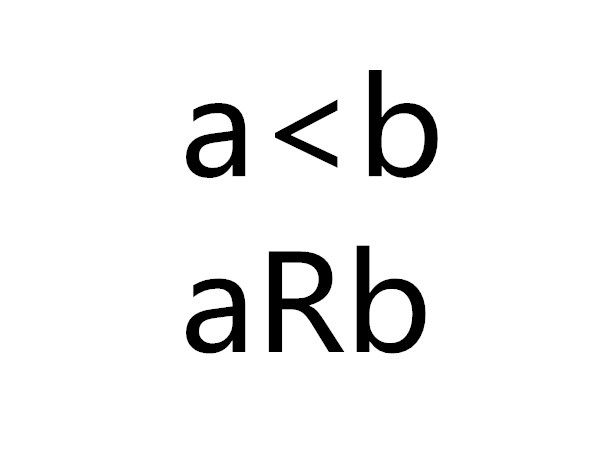
嚴格偏序關係(strictly partially ordered relation)是一種重要的偏序關係,集合X上的關係R若具有反自反性和傳遞性,則稱R為X上的一個嚴格偏序,記作<。
嚴格偏序關係(strictly partially ordered relation)是一種重要的偏序關係,集合X上的關係R若具有反自反性和傳遞性,則稱R為X上的一個嚴格偏序,記作<。基本介紹嚴格偏序關係是一種重要...
Ⅱ 反對稱性(即反對稱關係):對任意x,y∈A,若xRy,且yRx,則x=y;Ⅲ 傳遞性:對任意x, y,z∈A,若xRy,且yRz,則xRz。則稱R為A上的偏序關係,通常記作≼。注意這裡的≼不必是指一般意義上的“小於或等於”。若然有x≼y,我們也說x排在y前面(x precedes y)。偏序分類 非嚴格偏序,自反...
偏序集合定義了偏序拓撲。定義 設R是非空集合A上的一個二元關係,若R滿足: 自反性、反對稱性、傳遞性,則稱R為A上的偏序關係。以下為定義:非嚴格偏序,自反偏序 給定集合S,“≤”是S上的二元關係,若“≤”滿足:自反性:∀a∈S,有a≤a;反對稱性:∀a,b∈S,a≤b且b≤a,則a=b;傳遞性:...
1、aRb,若且唯若a到b有一條或幾條嚴格上升的線段或折線連結。a與b間無線連結,或雖有折線連結但在上下起伏的時候,且 。如圖1中 ,,,等(為R的補關係)。2、無水平的線段。3、當R是全序時,哈塞圖可畫成一個上升的鏈狀圖,如圖4。4、同一個集合,當偏序關係不同時,有不同的哈塞圖。例如,當A={2,...
序關係(ordering relation)也叫做“偏序關係”、“弱偏序關係”或“半序關係”是集合元素間的一種二元關係。設一非空集合S,其元素之間定義了一種二元關係→,若R滿足:1.不可逆性:對任意a,b∈S,若有a→b,則沒有b→a。2.傳遞性:對任意a,b,c∈S,若有a→b,b→c,則有a→c。3.有自反性:對...
偏序關係模型 偏序關係模型(partial order relational model)是2018年公布的計算機科學技術名詞。定義 針對偏序域數據(屬性的值域可以是偏序的資料庫)特性的一種擴展的關係數據模型。傳統關係模型中的關係、關係代數、函式依賴分別被擴展為序關係、序關係代數、序函式依賴。出處 《計算機科學技術名詞 》第三版。
我們可以通過這四個關係中的任何一個,定義或解釋集合全序的方式;由符號易知所談論的是非嚴格的,抑或是嚴格全序。全序關係與偏序關係 偏序和全序是公理集合論中的概念。首先需要知道什麼是二元關係。比如實數中的“大小”關係,集合的集合中的“包含”關係就是兩種二元關係。所謂偏序,即偏序關係,是一種二元關係。...
設集合(S,≤)為一全序集,≤是其偏序關係,若對任意的S的非空子集,在其序下都有最小元素,則稱≤為良序關係,(S,≤)為良序集。正反例子 1、自然數集在通常序下是良序集。2、整數集在通常序下不是良序集,例如該集合本身就沒有一個最小元素。3、整數的下列關係R是良序的:x R y,若且唯若下列條件...
二元關係的數目 在一個有n個元素的集合(簡稱n元素集)上,一共有 個可能的二元關係。註:反自反關係和自反關係的數目一樣多。嚴格偏序(反自反的傳遞關係)的數目和偏序的一樣多。全序即是那些同時是全預序的偏序。透過容斥原理的想法,可知那些既不是偏序也不是全預序的預序數目是:預序的數目,減去偏序的...
模糊偏序關係(fuzzy partially ordered relations)是論域X上的一個模糊關係,它滿足自反性、可傳遞性以及完全反對稱性,即當x≠y, R(x,y)>0時,必有R(y,x)=0。基本介紹 設 ,(1) 叫做具有模糊自反性,或者說 是模糊自反關係,是指,每個 ,都能使 。(2) 叫做具有模糊完全反對稱性,或者說 ...
擬序關係的逆關係一定是擬序的,反對稱的擬序關係是偏序關係,但擬序關係可以不是偏序關係。定義 擬序關係是一種次序關係,比偏序關係的限制更嚴格一些。它是一種滿足反自反、反對稱與傳遞的關係。設R是非空集合A上的關係,若R具有反自反性、傳遞性,則稱R是A上的擬序關係(Quasi-ordering relation),記該關係...
為偏序集, ,如果對任意的 ,都有 ,則稱 為單調遞增的;如果對任意的 ,都有 ,則稱 為嚴格單調遞增的。類似的,也可以定義單調遞減和嚴格單調遞減的函式。舉例分析 例1 單調遞增函式的一些例子:(1) 是嚴格單調遞增的;(2)偏序集 ,其中, 為包含關係,≤為一般的小於或等於關係。令 是單調...
(但請注意,“少於”是一種弱勢,導致總體秩序,即“小於或等於”,嚴格秩序與弱指令之間的關係在部分有序集上討論。)關係“是”的一個子集“也不是全部的,因為例如集合{1,2}和{3,4}都不是另一個的子集。特性 完全性蘊涵自反性。滿足傳遞性的全關係是弱序關係。滿足完全性的偏序關係是全序關係。
實數的嚴格小於關係 任意集合上的空關係(empty relation),即關係為空集時。整數上的整除關係|不是反對稱的(因為1|-1,-1|1,但1≠-1)。如果限制在自然數範圍內則是反對稱的。整數上的模n同餘是對稱的,但不是反對稱的。性質 按照定義,偏序和全序都是反對稱的。注意,反對稱關係不是對稱關係(aRb → ...
是集合間的一個嚴格偏序關係。包含和真包含關係定義了集合間的一個偏序關係。在該偏序關係的意義下兩者等價,通常不失一般性地將該偏序關係指為 。結構的定義 顯然,上面的所有結果並不是獨立的,大部分結果都可以從一個很小的結構推導出來。比如很容易知道:對稱差可以用並和差來定義。補可以用差來定義。真包含...
如果R是一嚴格偏序關係,那么R關係就可被表示為 如果我們將BT框架中的R關係具體化為滿足向下不分叉性的嚴格偏序關係 直觀來說,[α dstit:A]就表示結果事件A為真是行動者α的行動或者選擇來保證的且A並不是必然為真的;[α cstit:A]則只要求結果事件A為真是行動者α的行動或者選擇來保證的。
完全格一定不能混淆於完全偏序(cpo),它構成嚴格的更加一般的一個偏序集合類別。更特殊的完全格是完全布爾代數和完全Heyting代數(locale)。格 “格”一種特殊的偏序集。在許多數學對象中,所考慮的元素之間具有某種順序。例如,一組實數間的大小順序;一個集合的諸子集(或某些子集)間按(被包含)所成的順序 ;...
有向無環圖(DAG)的傳遞閉包是 DAG 的可到達性關係和一個嚴格偏序。與複雜性的關係 在計算複雜性理論中,複雜度類 NL 嚴格對應於可使用一階邏輯和傳遞閉包表達的邏輯句子的集合。這是因為傳遞閉包性質有密切關係於 NL-完全問題 STCON,找到在一個圖的有向路徑。類似的,類 L 是一階邏輯帶有交換傳遞閉包。在向...
集合A連同其上定義的偏序≤,稱為偏序集,記為〈A,≤〉。實數集上的通常的大小關係、集合之間的被包含關係、自然數之間的可整除關係都是偏序的例。設≤為A上的偏序。如果在A上定義一個關係 ①′對任何x∈A,x ②′由x 因此在偏序與嚴格偏序之中只需討論一種就夠了。設〈A,≤〉為一偏序集,如果x0∈A...
偏序關係 常見的序關係之一。若二元關係R滿足可傳性、反自反性,則稱R為一個嚴格偏序關係,通常記為。若 設〈A,R〉為一個偏序結構,C⊆A為A的非空子集,若a∈C∧ᗄx∈C(aR-x),則稱a為C的R極大元;若a∈C∧ᗄx∈C(xR-a),則稱a為C的R極小元;若a∈C∧ᗄx∈C(xRa∨x=a),則稱a...
10、對象X順序性說明(Sequential specification)定義為對象X的前綴閉的順序歷史集。順序性說明描述了一個對象所有可能的順序行為。11、合法的(Legal)順序歷史指的是 (指H中對象為x的那些事件)屬於x的順序性說明。線性一致性的形式化定義 對於給定的一個歷史H,其中必然蘊含著一個非自反的偏序關係 (可稱之為...
則屬性值確定對象間的不可分辨關係, 從而可建立以等價類為基本知識顆粒的Pawlak 粗糙集模型; 如果屬性值表達對象之間的相似程度(接近程度), 則可以通過定義相容關係, 以相容類或最大相容類為基本知識顆粒, 建立相容關係粗糙集模型[4-9];如果對象的屬性值表達對象之間的優勢關係(偏序關係), 則該系統被稱為序信息...
對任意集合S,為了證明存在S上的一個良序,令集合P為所有S的子集上的良序(嚴格來說,P的元素是S的子集和其上的良序關係組成的有序對)。對任意A,B∈P,定義A≤B若且唯若A是B的一個前段。(P,≤)構成一偏序集,且對這個偏序集的任意鏈,取其中所有良序的並,則得到這條鏈的一個上界。套用佐恩引理,...
序數是集合論基本概念之一,是日常使用的第一、第二等表示次序的數的推廣。序數概念是建立在良序集概念之上的,而良序集又是偏序集、全序集的特殊情形。序數類閉無界子集(closed unbounded subsetof class of ordinals)是序數類的一種子集。Ω的無界閉子集稱為Ω的閉無界子集。簡記為Ω的c.u.b。概念 序數類閉...
在考慮有向完全偏序或完全格的時候,規定上確界存在的額外的要求可以去掉。還要注意是有向完全的並半格幾乎就是完全格(可能缺乏最小元) -- 詳情參見完全性 (序理論)。如果存在的話,偏序集合的最小元總是緊緻的。它可能是唯一的緊緻元素,比如實數的單位區間 [0,1]。例子 最基本的例子是某個集合的冪集按照...
10.4.2 由關係圖、關係矩陣判別關係的性質 10.5 複合關係和逆關係 10.5.1 複合關係 10.5.2 複合關係的矩陣表示及圖形表示 10.5.3 逆關係 10.6 關係的閉包運算 10.7 等價關係與相容關係 10.7.1 集合的劃分和覆蓋 10.7.2 等價關係與等價類 10.7.3 相容關係 10.8 偏序關係 10.8.1 偏序關係的...
等價的說,假定某種選擇公理,一個二元關係稱為是良基的,若且唯若它不包含可數的無窮降鏈,也就是說不存在X的元素的無窮序列x₀,x₁,x₂, ...使得對所有的自然數n有著xₙRxₙ。在序理論中,一個偏序關係稱為是良基的,若且唯若它對應的嚴格偏序是良基的。如果這個序還是全序,那么此時稱這個序...
數學中,“格”一種特殊的偏序集。在許多數學對象中,所考慮的元素之間具有某種順序。群表示一個擁有滿足封閉性、結合律、有單位元、有逆元的二元運算的代數結構,包括阿貝爾群、同態和共軛類。格的概念 “格”一種特殊的偏序集。在許多數學對象中,所考慮的元素之間具有某種順序。例如,一組實數間的大小順序;一...
b(讀作“a嚴格後於b"):若b a。若S的元素a和b既不是a b又不是b a,它們是不可比較的。如果S的元素a嚴格在b之前,即a b,並且不存在S的元素x使得a x b,那么我們說a是b的一個直接前元,記作a b或 。關於偏序集以及直接前元等,有多種不同的記法。在下面哈塞(Hasse)圖表示的偏序集中...
