模糊偏序關係(fuzzy partially ordered relations)是論域X上的一個模糊關係,它滿足自反性、可傳遞性以及完全反對稱性,即當x≠y, R(x,y)>0時,必有R(y,x)=0。
基本介紹
- 中文名:模糊偏序關係
- 外文名:fuzzy partially ordered relations
- 所屬學科:數學
- 所屬問題:模糊集合論
- 簡介:論域X上的一個模糊關係
基本介紹




















相關介紹







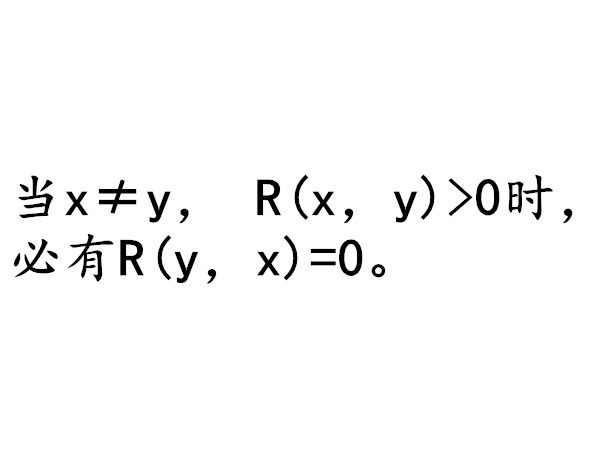
模糊偏序關係(fuzzy partially ordered relations)是論域X上的一個模糊關係,它滿足自反性、可傳遞性以及完全反對稱性,即當x≠y, R(x,y)>0時,必有R(y,x)=0。



























模糊偏序關係(fuzzy partially ordered relations)是論域X上的一個模糊關係,它滿足自反性、可傳遞性以及完全反對稱性,即當x≠y, R(x,y)>0時,必有R(y,x)=0。基本介紹設...
偏序關係模型 偏序關係模型(partial order relational model)是2018年公布的計算機科學技術名詞。定義 針對偏序域數據(屬性的值域可以是偏序的資料庫)特性的一種擴展的關係數據模型。傳統關係模型中的關係、關係代數、函式依賴分別被擴展為序關係、序關係代數、序函式依賴。出處 《計算機科學技術名詞 》第三版。
第4章敘述模糊值的運算與偏序關係。由於這裡的運算是基於模糊值的截集提出的,因此種類較廣,操作較易。第5章敘述模糊值間的距離與模糊距離概念,給出衡量或比較模糊值之間差異的一種手段。第6章則是在模糊值間距離基礎上,討論三類模糊值空間的一些拓樸性質,如完備性、連通性、列緊性及可分性。第7章敘述模糊值...
《模糊理論基礎(第2版)》是2010年6月武漢大學出版社出版的圖書,作者是胡寶清。本書系統地介紹了模糊集理論及其套用的基本原理與基本方法。作者簡介 胡寶清,男,1962年3月出生於湖北仙桃,武漢大學數學與統計學院教授、博士生導師。1982年獲得學士學位,學習基礎數學。1987年獲得碩士學位,主攻專業為模糊數學。2001年...
《格值模糊擬陣理論的進一步研究及其套用》是依託北京理工大學,由史福貴擔任項目負責人的面上項目。項目摘要 本項目擬在已有M-模糊化擬陣的基礎上,繼續研究M-模糊化擬陣的縱深問題. 除了考慮從已知M-模糊化擬陣出發構造新的M-模糊化擬陣的方法外,我們試圖藉助於模糊偏序集理論,探討M-模糊化擬陣的代數結構,研究...
§5.2模糊矩陣分解定理 §5.3布爾矩陣的冪收斂性 §5.4模糊矩陣的收斂定理 §5.5振盪模糊矩陣 第6章 常用模糊矩陣冪序列一致理論 §6.1k階迴路占優矩陣 §6.2 2階主元占優n×n模糊矩陣 §6_3蘊涵矩陣的收斂性 §6.4常用模糊矩陣收斂指數的一致上界 第7章 格與格上的矩陣 §7.1偏序集與格 §7....
該模型較經典意義上的模型更具有普遍意義。 (六)深入研究了模糊指派問題和聯盟收益為模糊數的Shapley值的解的問題。在基於模糊合作博弈的供應鏈風險分擔機制的數學模型中,經典的解題方法不適合處理其中的模糊指派問題和聯盟收益為模糊數的Shapley值的問題。論文通過引入了[x]+[a]=[b]的模糊方程與偏序的思想,...
第9章模糊偏序關係的信息系統 9.1評估決策的基本思想 9.2評估決策的模糊偏序模型 9.3模糊偏序關係上的信息融合 9.4互補一致模糊偏序關係的直接排序方法 第10章不完備信息系統 10.1不完備信息系統及其近似 10.2不完備信息系統的最優選擇 10.3不完備信息系統的優劣關係及決策規則 10.4不完備信息系統的優勢關係下...
3.6.2 模糊偏序關係支持度計算模型/114 3.6.3 FA-SDCM算法/116 3.6.4 FA-SDCM算法實驗/118 3.7 基於真值發現的衝突數據源質量評價算法/123 3.7.1 相關概念/123 3.7.2 數據源質量評價模型/125 3.7.3 TFDQ算法/125 3.7.4 TFDQ算法實驗/127 3.8 多源衝突數據融合研究成果在企業數據資源管理中...
筆者在心理學研究中特別留意心理學方法學的研究,注重用系統分析的科學方法來探究心理現象,將模糊聚類分析法、模糊偏序關係矩陣排列法、多特質多方法分析套用於人格研究。心理學之所以成為一門科學,最根本的是其研究方法的科學性。科學研究成果的基本特徵是,它具可操作性、可證偽性、可重複性和可爭辯性。用這個標準...
黃希庭,男,浙江溫嶺人,北京大學普通心理學專業研究生畢業,西南大學心理學部教授,博士生導師。在時間心理學方面:在中國開創了時間心理學研究;在人格心理學方面:對大學生心理進行了深入的研究,將模糊聚類分析法、模糊偏序關係矩陣排列法、多特質多方法分析、探索性因素分析和驗證法因素分析等套用於人格研究。湯永隆...
② 在中國開創了大學生心理學的研究,將模糊聚類分析法、模糊偏序關係矩陣排列法、多特質多方法分析、探索性因素分析和驗證法因素分析等套用於人格研究;最先把價值觀引入心理學教材;把價值觀劃分為十大類,即人生價值觀、政治價值觀、道德價值觀、人際價值觀、職業價值觀、審美價值觀、宗教價值觀、自我價值觀、婚戀...
第三,套用方面,主要針對與描述邏輯擴展和推理緊密相關的領域,如粗糙集和模糊集理論等進行了討論。給出了模糊偏序集範疇與完備L-格範疇之間的關係;引入了格上粗糙理想的概念,並證明了全體粗糙理想構成了一個代數的有頂交結構;給出了代數domain和代數L-domain的一種較為簡單的信息系統表示。
