商範疇

商範疇(quotient category)是代數系的商代數系及局部化的高度推廣。

範疇是範疇論的基本概念之一。商代數是一個代數結構模它的同餘關係產生的新的代數結構。一個代數結構必定與它的商代數同態，把任一元素對應到這個元素所在的等價類的映射就是代數結構到其商代數的同態映射。反過來，代數結構A的任何一個同態映射可以導出A的一個同餘關係～，並得到商代數A/～，A/～必與A的同態象同構。

基本介紹

• 中文名：商範疇
• 外文名：quotient category
• 領域：數學
• 學科：抽象代數
• 性質：範疇
• 對象：商代數

概念

商範疇(quotient category)是代數系的商代數系及局部化的高度推廣。若C為一個範疇，二元關係R對C中任兩個對象A，B的態射集Hom_C(A，B)都給出一個二元關係R_A，B，則必有一個範疇C/R(其對象類仍為C的對象類)，以及一個函子Q=Q_R：C→C/R使：

1.若f，f′∈Hom_C(A，B)且fR_A，Bf′，則Qf=Qf′.

2.若D為一個範疇，H：C→D是一個使fR_A，Bf′蘊含著Hf=Hf′的函子，則有惟一的函子H′：C/R→D使H′°Q=H.

3.函子Q關於對象是滿單的。

由二元關係R必可誘導一個使RR′的最小的二元關係R′，使對任意的A，B，R′_AB都是Hom_C(A，B)上的等價關係.於是按R′_A，B可得商集Hom_C(A，B)/R′_A，B.C/R關於A，B的態射集Hom_C/R(A，B)就取為Hom_C(A，B)/R′_A，B，態射合成按顯見的方式定義，這樣得出的範疇C/R稱為範疇C(關於R)的商範疇.例如取C=Top(對象為拓撲空間，態射為連續映射)，取R為同倫關係，則得C的商範疇C/R，它以拓撲空間A，B，…為對象，而Hom_C/R(A，B)則為A到B的連續映射之同倫類的集合。對局部小的阿貝爾範疇A，若B為A的塞爾子範疇，則可按下法定義一個範疇A/B，其對象類即A的對象類；其態射集(對任意的對象A，B)定義為：

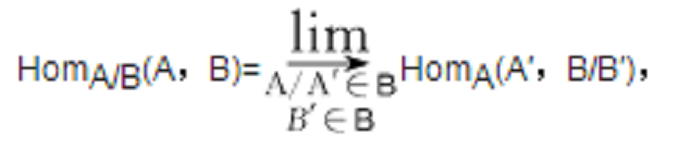
其中，表集範疇中的正向極限，態射合成按顯見方式定義。這個範疇A/B就稱為A關於B的商範疇。A/B仍為一個阿貝爾範疇。

範疇

範疇是範疇論的基本概念之一。稱C是一個範疇，是指C滿足下述六點：

1.C有一個對象類{A，B，C，…}(不要求它是一個集合，即不要求它滿足集合論的公理，只要求能判別出是不是它的對象)，常記為ObjC或簡記C。

2.對C的任兩對象A，B，有一個確定的集合(可為空集)Hom(A，B)，其元素稱為由A到B的態射，記為f∈Hom(A，B)或f：A→B。

3.對給定的f∈Hom(A，B)與g∈Hom(B，C)有惟一的gf∈Hom(A，C)，稱為f與g的合成。

4.Hom(A，B)與Hom(C，D)有公共元是指A=C且B=D。

5.態射合成滿足結合律。

6.對C的任意對象A，Hom(A，A)至少有一個元素ε_A使對σ∈Hom(A，B)恆有σε_A=σ=ε_Bσ，稱ε_A為A的恆等態射(ε_B為B的恆等態射)。

例如，以一切集合作對象，以集合映射作態射，則得集合範疇Set(簡稱集範疇)。以一切拓撲空間作對象，以連續映射作態射，則得拓撲空間範疇Top。以一切環為對象，以環同態作為態射得環範疇Ring。類似地，可得群範疇Group，阿貝爾群範疇AG，環R上的左R模範疇_RM等。以自然數為對象，a|b(表示a整除b)時定義Hom(a，b)有惟一元素φ_ab，ab時定義Hom(a，b)=(空集)，也得到一個範疇.一般地，對每個擬序集都可仿此定義範疇。

商代數

商代數是一個代數結構模它的同餘關係產生的新的代數結構。

集A上的等價關係～將A劃分成互不相交的等價類的並，記成=A/～，即的元素[a]是a所在的等價類。稱為A關於～的商集。進一步，設～是代數結構〈A，◦〉上的等價關係，並且對任意a，b∈A，若a～b，對任何c∈A，都有a◦C～b◦c，且c◦a～c◦b，則稱等價關係～是〈A，◦〉上的同餘關係。例如，模m同餘，a≡b (modm)，若且唯若m| (a-b)，是〈Z，+〉上的一個同餘關係，並且模m同餘也是〈Z，+，·〉上的同餘關係。又如，群〈G，·〉的正規子群N確定的陪集關係R，aRb若且唯若ab∈N，是〈G，+〉上的同餘關係。

設～是代數結構〈A，◦〉上的同餘關係，則可在商集=A/～上定義運算*。

[a₁] * [a₂]=[a₁·a₂]

稱代數結構〈A/～，*)=〈，* 〉為〈A，◦〉(關於～)的商代數。

例如，剩餘類環〈Z_m，+，·〉是〈Z，+，·〉的一個商代數，群〈G，·〉關於正規子群N的商群〈G/N·〉就是由N確定的陪集關係確定的商代數。

一個代數結構必定與它的商代數同態，把任一元素對應到這個元素所在的等價類的映射就是代數結構到其商代數的同態映射。反過來，代數結構A的任何一個同態映射可以導出A的一個同餘關係～，並得到商代數A/～，A/～必與A的同態象同構。

模範疇

模範疇(category of modules)是一種重要的範疇。指所有以模和模之間的同態組成的範疇。利用範疇的觀點來討論模和環是一種重要方法。若A是環，則所有的左A模組成的類和所有左A模M，N之間的模同態Hom_A(M，N)，以及模的同態的乘法運算法則構成一個範疇，稱為左A模範疇，記為：A-Mod。

同態

設E與F為兩個群胚，它們的合成法則分別記為⊥與⊤。 稱從E到F中的映射f是群胚同態，如果對於E的任一元素偶(x，y)，有：

設E與F為兩個么半群(兩個群)，稱從E到F中的映射。f是么半群(群)的同態，如果f是群胚的同態，且E的中性元素的象是F的中性元素。(在群的情況下，後一個條件是自然滿足的，但是從加法么半群N到乘法么半群N的映射x↦0是群胚的同態， 而並不因此就是么半群的同態)。

設G為乘法群，而a為G的元素。由關係f(n)=an所定義的從加法群Z到G中的映射f是群的同態。

設A與B為兩個環(兩個體)，稱從A到B中的映射f是環(體)的同態，如果f是加法群的同態，且為乘法么半群的同態。這就是說，對A的任一元素偶(x，y)，有

f(x+y)=f(x)+f(y)f(xy)=f(x)f(y)，

並且f將A的單位元變成B的單位元。

例如，設n為非零自然數；使任一有理整數對應其對模n的剩餘類映射是從環Z到環Z/nZ上的同態。設E與F為兩個A-代數(兩個酉A-代數)。稱從E到F中的映射f是A-代數(酉A-代數)的同態，如果它是線性映射，並且是乘法群胚(乘法么半群)的同態。

例如，設E為交換體K上的非零有限n維向量空間，而B為E的基。則從E的全體自同態之酉代數ℒ(E)到K中元素構成的全體n階方陣之酉代數Mn (K)中的映射，如果該映射使E的任一自同態對應它在基B中的矩陣，則這一映射是酉代數的同態。

同態的概念能用抽象的方式加以推廣。