哈代不等式(Hardy inequality)是與二重級數有關的不等式,即哈代(G.H.Hardy)研究二重級數時,於1920年建立的不等式。
基本介紹
- 中文名:哈代不等式
- 外文名:Hardy inequality
- 所屬學科:數學
- 提出者:哈代(G.H.Hardy)
- 提出時間:1920年
- 簡介:與二重級數有關的不等式
基本介紹

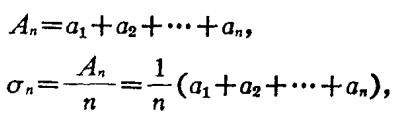












哈代不等式的證明






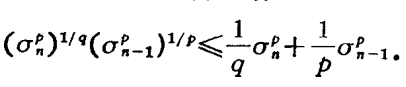




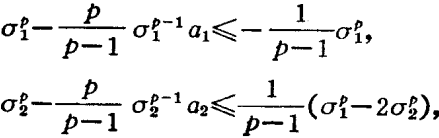
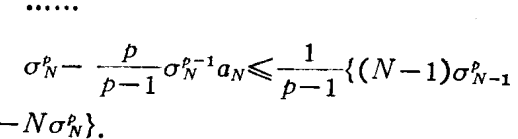
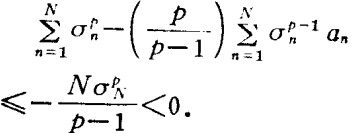
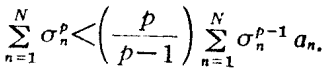


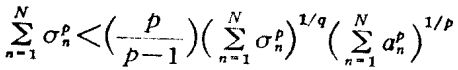


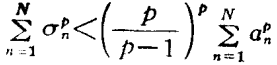


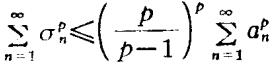
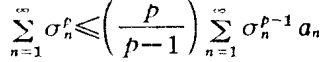
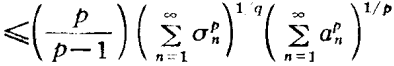













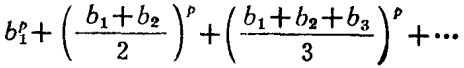
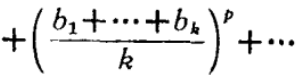
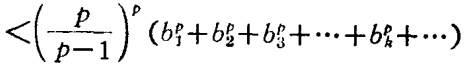

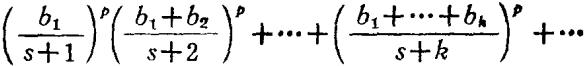
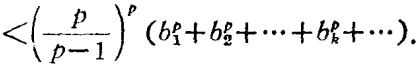



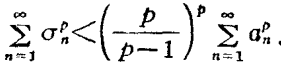

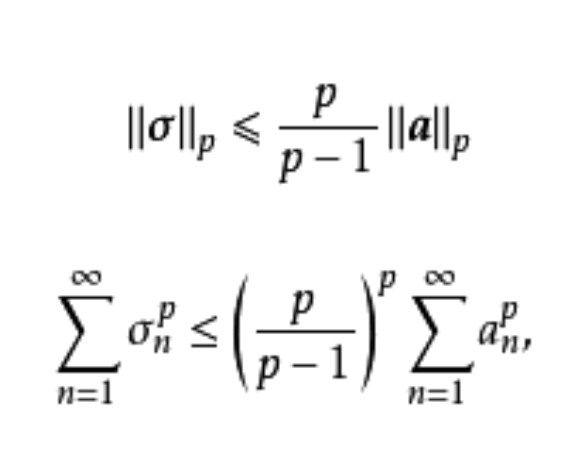
哈代不等式(Hardy inequality)是與二重級數有關的不等式,即哈代(G.H.Hardy)研究二重級數時,於1920年建立的不等式。

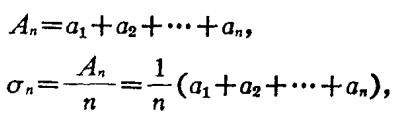


















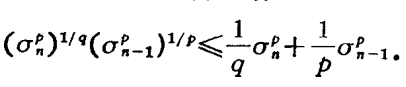




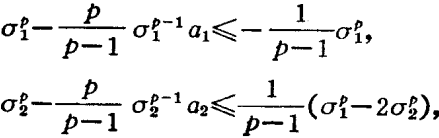
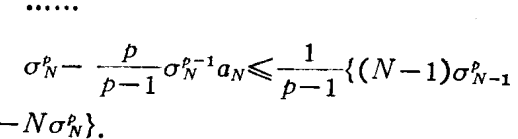
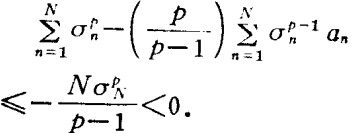
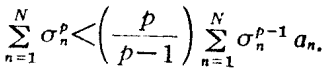


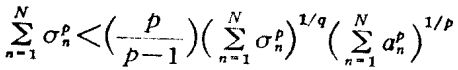


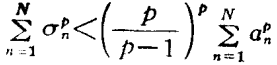


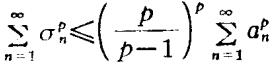
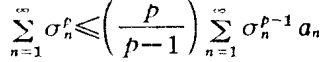
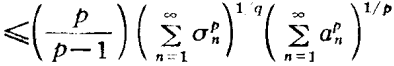













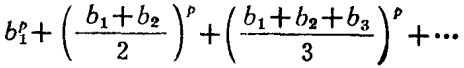
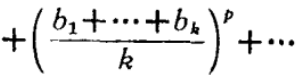
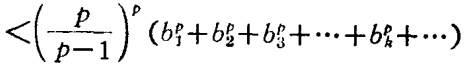

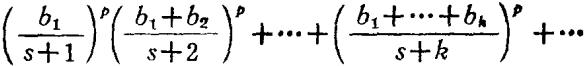
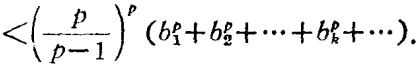



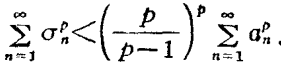

哈代不等式(Hardy inequality)是與二重級數有關的不等式,即哈代(G.H.Hardy)研究二重級數時,於1920年建立的不等式。基本介紹設a=(a1,a2,…,an…)是給定的無窮維向量,記A0=0,=0....
《不等式第2版》2020年7月人民郵電出版社出版的圖書。作者是[英]戈弗雷·哈代、 [英]約翰·李特爾伍德、 [美]喬治·波利亞。本書是哈代、李特爾伍德、波利亞合著的一部經典之作。。內容簡介 本書是哈代、李特爾伍德、波利亞合著的一...
哈代長李特爾伍德8歲,他們結識於1904年,在長達35年的合作中,聯名發表了約100篇論文,其中包括丟番圖逼近、堆壘數論、數的積性理論、黎曼ξ函式、不等式、一般積分、三角級數等廣泛的內容。哈代-李特爾伍德極大函式,哈代-李特爾伍德圓...
《Heisenberg 群哈代空間上的乘子定理與哈代不等式》是依託廣東石油化工學院,由肖勁森擔任項目負責人的數學天元基金項目。項目摘要 歸因於Heisenberg群在數學方面的幾何背景和在物理方面的量子力學背景,越來越多的研究希望調和分析在Heisenberg...
3.6 逆向的希爾伯特型積分不等式及相關的運算元表示 3.7 若干特例及基本的希爾伯特型積分不等式 3.8 一般齊次核的哈代型積分不等式及其運算元刻畫 3.9 一般非齊次核的希爾伯特型積分不等式及其運算元刻畫 3.10 一般非...
此不等式是T.Carleman於1923年得到的。卡萊曼不等式的證明 Carleman不等式:設 為正數,記 的幾何平均值為G(i=1,2,…,,n),則 證明 事實上,若在哈代-蘭道不等式(Hardy-Landau不等式)中用 代替 ,則得 令 ,則因 所以...
柯特拉不等式是考爾德倫-贊格蒙運算元與哈代-李特爾伍德極大運算元間的關係式。簡介 柯特拉不等式是考爾德倫-贊格蒙運算元與哈代-李特爾伍德極大運算元間的關係式。具體內容 設 T 是考爾德倫-贊格蒙運算元 ,K(x,y)是其積分核,對任意ε>0,...
逆向赫爾德不等式(inverse Holder inequality)是Aₚ類中權函式的一種重要性質。簡介 逆向赫爾德不等式是Aₚ類中權函式的一種重要性質。設ω(x)∈Aₚ,那么存在常數C>0,δ>0,使對任意的立方體Q⊂Rⁿ,有 套用 滿足逆向...
他還著有《一個數學家的辯白》《不等式》《哈代數論》等,這三本書均已由圖靈公司出版中譯本,後兩本已終止銷售,近期計畫再版。目錄 第 1章 實變數 第 2章 實變函式 第3章 複數 第4章 正整變數函式的極限 第5章 一個連續...
哈代-李特爾伍德極大函式,也經常被引用。出版著作 李特爾伍德與哈代合作寫了100多篇論文,其它著作有:《函式論教程》(1944)《不等式》(1934年初版,1952年修訂版,與哈代、波伊亞合作.中譯本科學出版社1965年出版)
用三角不等式有 設 。(Mh為h的哈代-李特爾伍德極大函式。)從上式得 因為 ,所以有 若Tf>y,則有Mh>y/2或者|h| >y/2。因此 由哈代-李特爾伍德極大不等式得 由積分的基本性質有 ,故得 。因此 因為上式對所有正...
華氏不等式 1936年華羅庚到劍橋大學進修了兩年,他師從哈代,積極參加劍橋大學數論小組的學術討論班活動,迅速進入到該領域前沿。華羅庚潛心研究數論的重要問題,解決了華林(Waring)問題,他利(Tarry)問題等數學難題,其傑出才華在劍橋沃土...
這一族球的半徑上確界是2,然而全部球的半徑都小於2。若選任何一個 為這個子集,因有半徑更大的球 在原點的另一側,故此 不覆蓋 。套用 這條引理可用於證明哈代-李特爾伍德極大不等式。參見 貝西科維奇覆蓋定理 ...
這一相容性定理,可用於直接證明線性規劃的對偶定理等,成為線性規劃論的一塊基石。另外,它還能簡單地導出許多著名的不等式,例如哈代(Hardy)-李特爾伍德(Littlewood)-波利亞(Polya)關於最佳化(majorization)的不等式。凸函式基本定理 ...
《數學奧林匹克中的不等式研究》序 不等式在數學中占有重要的地位。自1934年哈代、立特武德、波利亞的名著《不等式》(越民義譯,科學出版社,1965)問世以來,有關不等式問題的研究層出不窮,文章、著作也很多。如Beckenbach,Bellman《...
華羅庚在國際上以華氏命名的數學科研成果就有“華氏定理”、“懷依-華不等式”、“華氏不等式”、“普勞威爾-加當華定理”、“華氏運算元”、“華-王方法”等 [10] [16]。 20世紀40年代,華羅庚解決了高斯完整三角和的估計這一歷史難...
