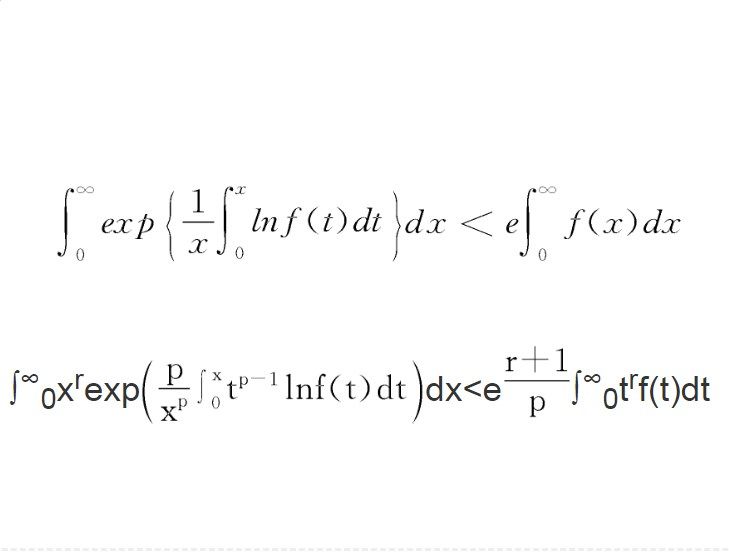卡萊曼不等式(Carleman inequality)是關於項為乘積冪的級數的估計式及其推廣,這個不等式由卡萊曼(T.Carleman)於1923年發表。
基本介紹
- 中文名:卡萊曼不等式
- 外文名:Carleman inequality
- 所屬學科:數學
- 所屬問題:數學分析(不等式)
- 發現者:T.Carleman
- 發現時間:1923年
- 簡介:關於項為乘積冪的級數的估計式
基本介紹,卡萊曼不等式的證明,
基本介紹
卡萊曼(Carleman)不等式 (1)如果 是任意非負數列,那么
是任意非負數列,那么





此不等式是T.Carleman於1923年得到的。
卡萊曼不等式的證明

證明
事實上,若在哈代-蘭道不等式(Hardy-Landau不等式)中用 代替
代替 ,則得
,則得





另外,不等式(1)也可用Redheffer不等式得到:
令 ,這裡
,這裡 ,則
,則