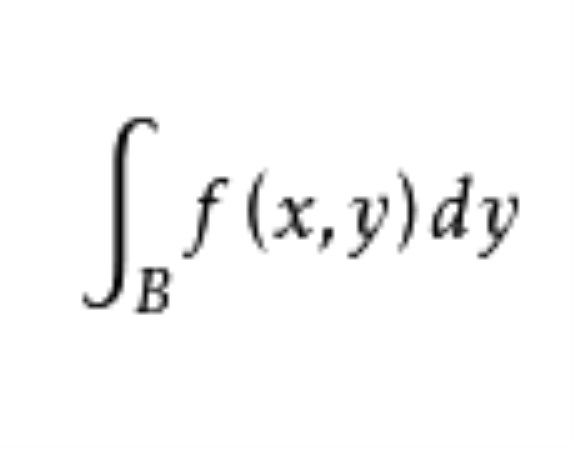含參量積分

含參量積分(integral with parameters)是多元函式對其一部分自變數的積分。設f(x，y)為定義在矩形區域R=[a，b]×[c，d]上的二元函式，若對於[a，b]上每一固定的x值，f(x，y)作為y的函式在閉區間[c，d]上可積，則其積分值是x在[a，b]上取值的函式，記作I(x)，即I(x)=∫_cf(x，y)dy，(x∈[a，b])，函式I(x)稱為定義在[a，b]上含參量x的正常積分，簡稱含參量積分；設f(x，y)為定義在區域G={(x，y)|c(x)≤y≤d(x)，a≤x≤b)上的二元函式，其中c(x)，d(x)為定義在[a，b]上的連續函式，若對於[a，b]上每一固定的x值，f(x，y)作為y的函式在閉區間[c(x)，d(x)]上可積，則其積分值是x在[a，b]上取值的函式，記作F(x)，即F(x)=∫_c(x)f(x，y)dy，(x∈[a，b])，函式F(x)也稱為定義在[a，b]上含參量x的正常積分，簡稱含參量正常積分。設函式f(x，y)定義在無界區域R=[a，b]×[c，+oo)上，若對每一個固定的x∈[a，b]，反常積分∫_cf(x，y)dy都收斂，則它是x在[a，b]上取值的函式，記作I(x)，即I(x)=∫_cf(x，y)dy，(x∈[a，b])，稱式∫_cf(x，y)dy為定義在[a，b]上的含參量x的無窮限反常積分，簡稱含參量反常積分。

基本介紹

• 中文名：含參量積分
• 外文名：integral with parameters
• 所屬學科：數學
• 所屬問題：數學分析
• 簡介：多元函式對其一部分自變數的積分

基本介紹

含參量積分是多元函式對其一部分自變數的積分，即形如

的積分，其中y=(y₁，y₂，…，y_m)∈BR，x=(x₁，x₂，…，x_n)∈AR，f是實函式，當這個積分作為常義或反常積分有意義時，分別稱為含參量常義或廣義積分，x是其參量.這時它定義了一個A上的實函式：

φ(x)=∫_Bf(x，y)dy.

含參量積分理論的主要內容就是研究這個函式的連續性、可微性、可積性，並在可能的情況下求出這個函式以及利用含參量積分計算定積分或表示一些超越函式。

含參量積分的主要性質

下面就f是二元函式情況(即只含一個參量的積分)略述含參量積分的一些主要性質.

1.含參量的常義積分的性質：

1) 若f在D={(x，y)|a≤x≤b，c≤y≤d}上連續，則由積分定義的函式

在[a，b]上連續。

2) 若f在D上可微，f_x(x，y)，f_y(x，y)在D上連續，則φ(x)在[a，b]上連續可微，且

2.含參量的無窮積分的性質：

1) 若f在E={(x，y)|a≤x≤b，c≤y<+∞}上連續，且

關於x在[a，b]上一致收斂，則由此積分定義的函式在[a，b]上連續。

2) 若f及f_x(x，y)在1)中E上連續，存在x₀∈[a，b]，使

收斂，且

關於x在[a，b]上一致收斂，則

在[a，b]上處處可微，且可以在積分號下求導數，即

3) 若f(x，y)及相應積分滿足1)的條件，則

4) 若f在F={(x，y)|a≤x<+∞，c≤y<+∞}上連續，

則

為有限數。

以上各條性質對於瑕積分均成立，只需對條件和結論作相應的修改即可。含參量的廣義積分的收斂概念、收斂判別法及有關性質與函式項級數極為相似。