設W是數域F上的向量空間V的一個非空子集,若W對於V的加法和數量乘法具有封閉性,則稱W是V的一個向量子空間,簡稱子空間。
基本介紹
- 中文名:向量子空間
- 外文名:vector subspace
- 套用學科:數學術語
- 範疇:數理科學
- 涉及:向量空間
- 簡稱:子空間
定義


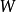




性質






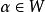
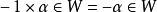




例子

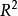



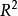




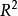

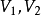

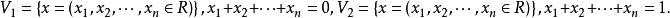

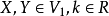
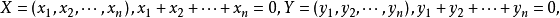
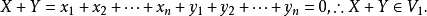



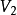

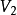

設W是數域F上的向量空間V的一個非空子集,若W對於V的加法和數量乘法具有封閉性,則稱W是V的一個向量子空間,簡稱子空間。


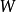










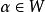
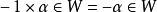





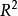



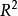




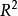

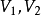

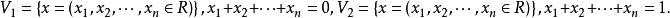

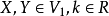
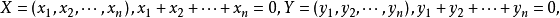
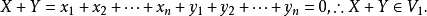



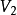

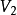
設W是數域F上的向量空間V的一個非空子集,若W對於V的加法和數量乘法具有封閉性,則稱W是V的一個向量子空間,簡稱子空間。...
線性子空間(又稱向量子空間,簡稱子空間)是線性空間中部分向量組成的線性空間。設W是域P上的線性空間V的一個非空子集合,若對於V中的加法及域P與V的純量乘法...
對於線性空間V,dim span{a1,a2……an}=rank{a1,a2……an},也就是說span是線性空間V其中的一個最大無關組時,則稱該子空間為生成線性子空間。設向量組{α...
子空間有多個意義,出現在不同領域。在數學上,子空間指的是維度小於全空間的部分空間。所謂空間,所指為帶有一些特定性質的集合,是故子空間可以算是子集合。在...
設L是線性空間H的線性子空間,如果L中一切向量都是零性的,則稱L是H的零性子空間。...... 設L是H的線性子空間,如果L中一切向量都是零性的,則稱L是H的零性...
向量空間又稱線性空間,是線性代數的中心內容和基本概念之一。在解析幾何里引入向量概念後,使許多問題的處理變得更為簡潔和清晰,在此基礎上的進一步抽象化,形成了與...
設L是線性空間H的線性子空間,子空間L若滿足L∩L⊥={0},則稱L是非退化的。...... 線性子空間(又稱向量子空間,簡稱子空間)是線性空間中部分向量組成的線性空...
賦范空間中的按範數導出的距離還是閉的線性子空間稱為閉線性子空間。...... 量乘法構成域P上的一個線性空間,則稱W為V的線性子空間(或向量子空間),或簡稱子空...
設x1,x2,...,xr(r>0)是V的r個向量,他們所有可能的線性組合所成的集是V的一個子空間,稱為x1,x2,...,xr張成的子空間。...
子空間疊代法也稱同時疊代法,它是乘冪法的直接推廣,能同時求出模較大的一些特徵值和相應的特徵向量。與乘冪法的區別主要在兩個方面:第一,同時疊代法是同時用幾...
如果A是矩陣,它的零空間就是所有向量的空間的線性子空間。這個線性子空間的維度叫做A的零化度(nullity)。這可以計算為在矩陣A的行梯陣形式中不包含支點的縱列數...
[1] 如果給定向量的起點(A)和終點(B),可將向量記作AB(並於頂上加→)。在空間直角坐標系中,也能把向量以數對形式表示,例如xOy平面中(2,3)是一向量。 在...
若矩陣A=[a1,a2,…,an]∈Cm×n為復矩陣,則其列向量的所有線性組合的集合構成一個子空間,稱為矩陣A的列空間(column space)或列張成(column span),用符號...
實數體R上的向量空間叫實向量空間。並且定義了加法和標量乘法這兩種運算。...... 實數體R上的向量空間叫實向量空間。並且定義了加法和標量乘法這兩種運算。[1] ...
數學中,一個辛向量空間是帶有辛形式ω 的向量空間 V,所謂辛形式即一個非退化斜對稱的雙線性形式。...
向量叢子叢指向量叢中全空間的子空間,它在一定條件下對於同一底空間按自然方式做成的向量叢。...
多線性子空間學習(Multilinear subspace learning)是一種通過直接映射高維張量(Tensor)數據到低維空間的一種降維(dimensionality reduction)方法。...
設H為線性空間,[·,·]是H上的一個雙線性埃爾米特泛函,x∈H,當x分別滿足[x,x]>0時,稱x為正性向量。...
所有k-向量生成的Λ(V)的子空間稱為V的k-階外冪,記為Λ(V)。外代數可以寫作每個k階冪的直和:該外積有一個重要性質,就是k-向量和l-向量的積是一個k+...
零化子空間是m維向量空間的與雙線性函式相聯繫的一種子空間。對確定的n維列向量X,滿足f=X'AY=0的m維列向量Y的全體構成m維向量空間P’的子空間,稱為f的零化子...
在數學裡,任何向量空間V都有其對應的對偶向量空間(或簡稱為對偶空間),由V的線性泛函組成。此對偶空間俱有一般向量空間的結構,像是向量加法及標量乘法。由此定義的...
