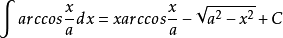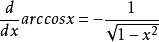基本介紹
概述,命名,定義,性質,
概述
在三角學中,反餘弦被定義為一個角度,也就是反余值的反函式,然而餘弦函式不是雙射且不可逆的而不是一個對射函式(即多個值可能只得到一個值,例如1和所有同界角),故無法有反函式,但我們可以限制其定義域,因此,反餘弦是單射和滿射也是可逆的,另外,我們也需要限制值域,且限制值域時,不能和反正弦定義相同的區間,因為這樣會變成一對多,而不構成函式,所以我們將反餘弦函式的值域定義在[0,π]。另外,在原始的定義中,若輸入值不在區間[-1, 1],是沒有意義的,但是三角函式擴充到複數之後,若輸入值不在區間[-1, 1],將傳回複數。
命名
定義
在復變分析中,反餘弦是這樣定義的:
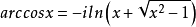
這個動作使反餘弦被推廣到複數。
性質
反餘弦函式是一個定義在區間[-1,1]的嚴格遞減連續函式。

其圖形是關於點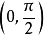 對稱的,所以滿足
對稱的,所以滿足 ;
;

反餘弦函式的不定積分是: