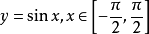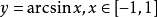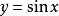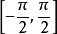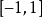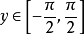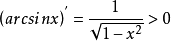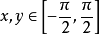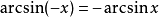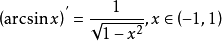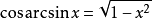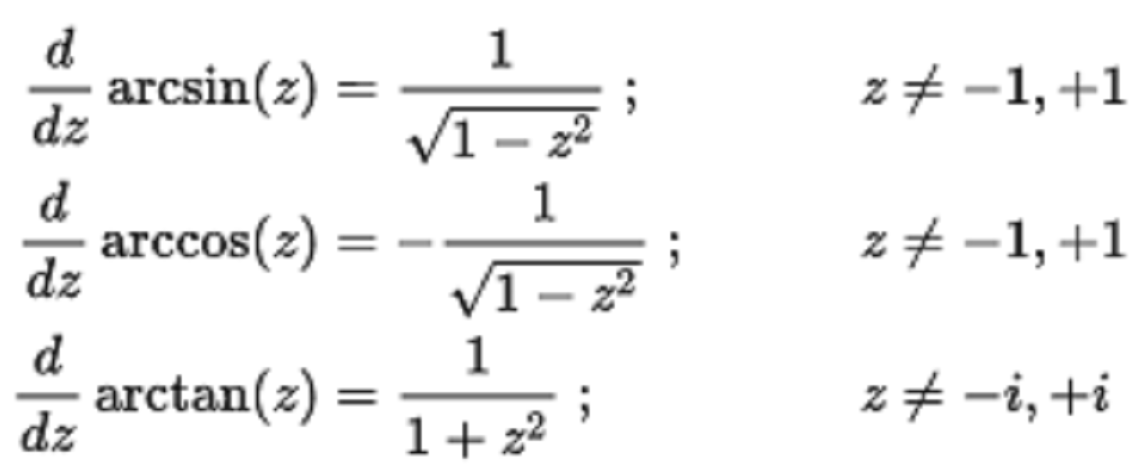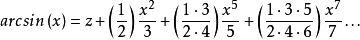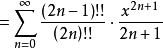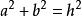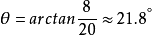在數學中，反三角函式（antitrigonometric functions），偶爾也稱為弓形函式（arcus functions），反向函式（reverse function）或環形函式（cyclometric functions））是三角函式的反函式（具有適當的限制域）。 具體來說，它們是正弦，餘弦，正切，餘切，正割和輔助函式的反函式，並且用於從任何一個角度的三角比獲得一個角度。 反三角函式廣泛套用於工程，導航，物理和幾何。
反正弦函式（反三角函式之一）為正弦函式y=sinx（x∈[-½π,½π]）的反函式，記作y=arcsinx或siny=x（x∈[-1,1]）。由原函式的圖像和它的反函式的圖像關於一三象限角平分線對稱可知正弦函式的圖像和反正弦函式的圖像也關於一三象限角平分線對稱。
基本介紹
- 中文名：反正弦函式
- 外文名：Arcsin function
- 表達式：y=arcsinx
- 學科：數學
- 定義域：[-1,1]
- 值域：[-π/2，π/2]
- 相關名詞：反餘弦函式
簡介,公式,圖像,性質,微分性態,套用,
簡介
在數學中，反三角函式（偶爾也稱為弓形函式（arcus functions），反向函式（antitrigonometric functions）或環形函式（cyclometric functions）是三角函式的反函式（具有適當的限制域）。 具體來說，它們是正弦，餘弦，正切，餘切，正割和輔助函式的反函式，並且用於從任何一個角度的三角比獲得一個角度。 反三角函式廣泛套用於工程，導航，物理和幾何。
反正弦函式（反三角函式之一）為正弦函式y=sinx（x∈[-½π,½π]）的反函式，記作y=arcsinx或siny=x（x∈[-1,1]）。由原函式的圖像和它的反函式的圖像關於一三象限角平分線對稱可知正弦函式的圖像和反正弦函式的圖像也關於一三象限角平分線對稱。
公式
用x表示自變數，用y表示因變數（函式值）時，正弦函式
的反函式叫做反正弦函式，記作
圖像
由原函式的圖像和它的反函式的圖像關於一三象限角平分線對稱，知正弦函式的圖像和反正弦函式的圖像也關於一三象限角平分線對稱。
作圖：先畫出函式
在
上的圖像，用平板玻璃或透明紙描好圖像，翻轉過來。（如圖所示）
性質
定義域
反正弦函式的定義域為
值域
反正弦函式的值域
單調性
反正弦函式是單調遞增函式。
證明。法一：
因為
證畢。
法二：令
且
，
因為
即
於是正弦函式在該區間上為增函式。所以，由反函式的性質，反正弦函式為增函式。
證畢。
奇偶性
反正弦函式是奇函式。即
證明。知在反正弦函式的值域上，正弦函式是奇函式，則反正弦函式也是奇函式。證畢。
導函式
反正弦函式的導函式
且
運算性質
反三角函式的三角函式如下式所示。 推導它們的一個快速方法是通過考慮直角三角形的幾何形狀，其長度為1的一側，長度x的另一側（0和1之間的任何實數），然後套用勾股定理和三角比。
反三角函式之間的關係
互補角度：
負參數：
倒數參數：
微分性態
反三角函式的導數
z的複數值的導數如下：
無窮級數
套用
找到一個直角三角形的角度
當三角形邊的長度已知時，當嘗試確定直角三角形的剩餘兩個角度時，反三角函式是有用的。 回想起正三角形的正確定義，例如，
通常，斜邊是未知的，需要使用勾股定理定理在使用反正弦或反曲線之前進行計算：
其中h是斜邊的長度。 在這種情況下，反正切是有用的，因為斜邊的長度是不需要的。
例如，假設當屋頂耗盡20英尺時，屋頂會下降8英尺。 屋頂與水平面形成一個角度θ，其中θ可以如下計算：
數值精度
對於0和π附近的角度，從而計算出計算機實現中精度降低的角度（由於位數有限）. 類似地，對於π/ 2和π/ 2附近的角度，反正弦不準確。
